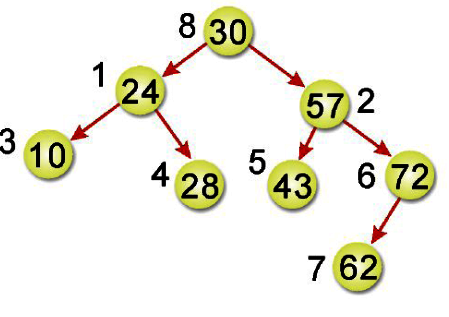
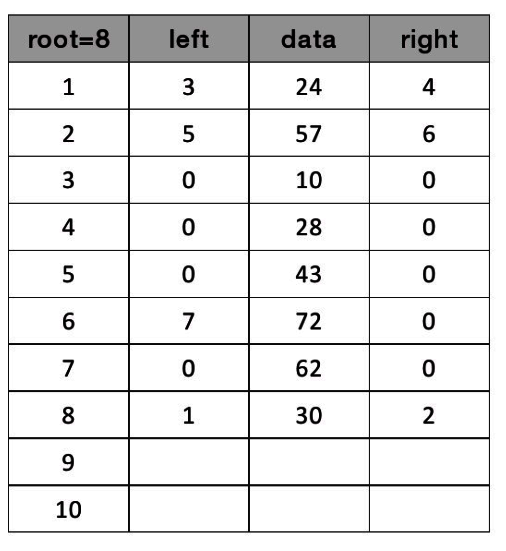
9-5二元樹節點插入
談到二元樹節點插入的情況和搜尋相似,重點是插入後仍要保持二元搜尋樹的特性。如果插入的節點在二元樹就沒有插入的必要,而搜尋失敗的狀況,就是準備插入的位置。
if (search (ptr, data)!=null)
process.stdout.write(‘二元樹中有此節點了!\n’)
else {
ptr=create_tree(ptr.data);
inorder(ptr);
}

JS add_search.js
class tree {
constructor () {
this.data=0;
this.left=0;
this.right=0;
}
}
var create_tree=(root, val)=> {
newnode=new tree();
newnode.data=val;
newnode.left=null;
newnode.right=null;
if (root==null) {
root=newnode;
return root;
}
else {
current=root;
while (current!=null) {
backup=current;
if (current.data>val)
current=current.left;
else
current=current.right;
}
if (backup.data>val)
backup.left=newnode;
else
backup.right=newnode;
}
return root;
}
var search=(ptr, val)=> {
while (true) {
if (ptr==null)
return null;
if (ptr.data==val)
return ptr;
else if (ptr.data>val)
ptr=ptr.left;
else
ptr=ptr.right;
}
}
var inorder=(ptr)=> {
if (ptr!=null) {
inorder(ptr.left);
process.stdout.write('['+ptr.data+'] ');
inorder(ptr.right);
}
}
arr=[7,1,4,2,8,13,12,11,15,9,5];
ptr=null;
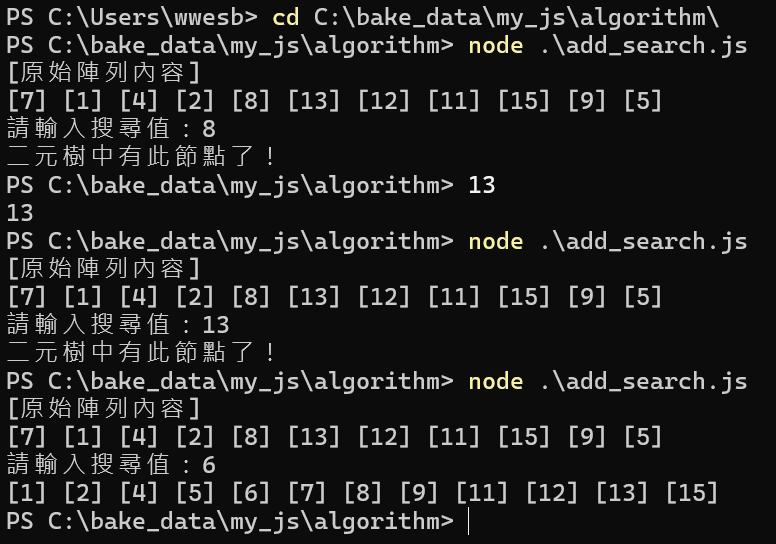
process.stdout.write('[原始陣列內容]\n');
for (i=0; i<11; i++) {
ptr=create_tree(ptr,arr[i]);
process.stdout.write('['+arr[i]+'] ');
}
process.stdout.write('\n');
const prompt=require('prompt-sync')();
const data=parseInt(prompt('請輸入搜尋值:'));
if (search(ptr,data) !=null)
process.stdout.write('二元樹中有此節點了!\n');
else {
ptr=create_tree(ptr,data);
inorder(ptr);
}
9-6二元樹節點的刪除
二元樹節點的刪除則稍微複雜,可分為以下三種狀況:
>刪除的節點為樹葉
只要將其相連的父節點指向null即可。
>刪除的節點只有一棵子樹
如下圖刪除節點1,就將其右指標欄放到其父節點的左指標欄:
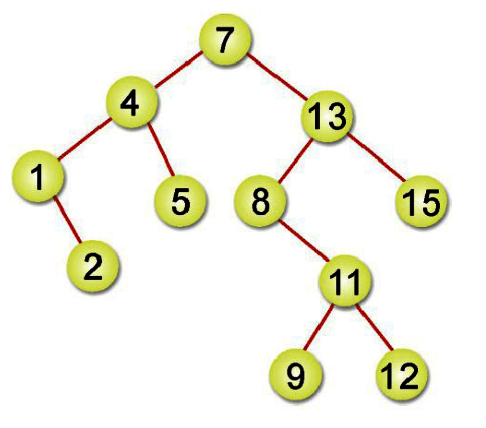
>刪除的節點有兩棵子樹
如下圖刪除節點4,方式有兩種,雖然結果不同,但都可符合二元樹特性:
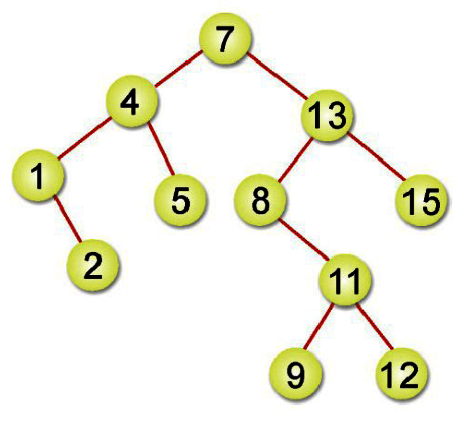
1.找出中序立即前行者(inorder immediate successor),即是將欲刪除節點的左子樹最大者向上提,在此即為節點2,簡單來說,就是在該節點的左子樹,往右尋找,直到右指標為null,這個節點就是中序立即前行者。
2.找出中序立即後繼者(inorder immediate successor),即是將欲刪除節點的右子樹最小者向上提,在此即為節點5,簡單來說,就是在該節點的右子樹,往左尋找,直到左指標為null,這個節點就是中序立即後繼者。

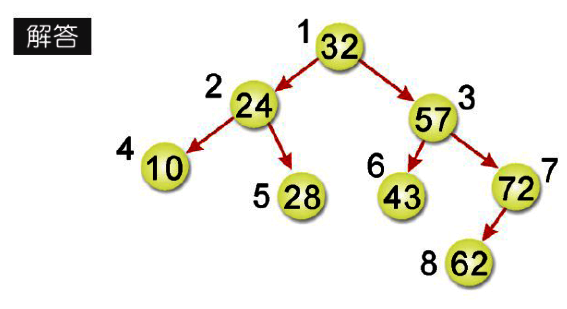
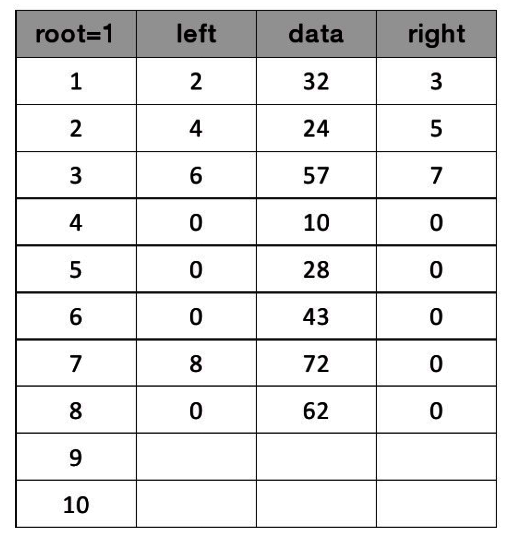
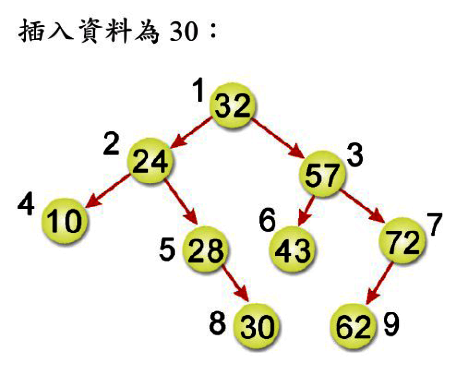
解法:
30<32 -> 所以往左邊。
30>24 -> 所以往右邊。
30>28 -> 所以往右邊。
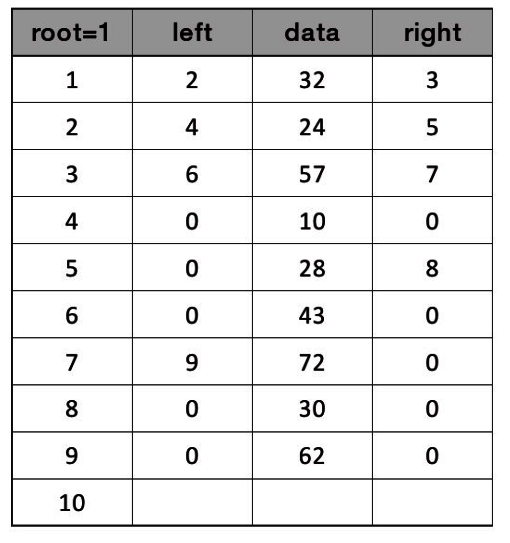
刪除的資料32:

解法:
方法1:中序後繼者->左子樹最大者:左子樹後往右邊找到最大,為節點8 數字30。
方法2:中序後繼者->右子樹最小者:右子樹往左找,碰到左右都有往左邊找,為節點6 數字43。