6-4八皇后演算法
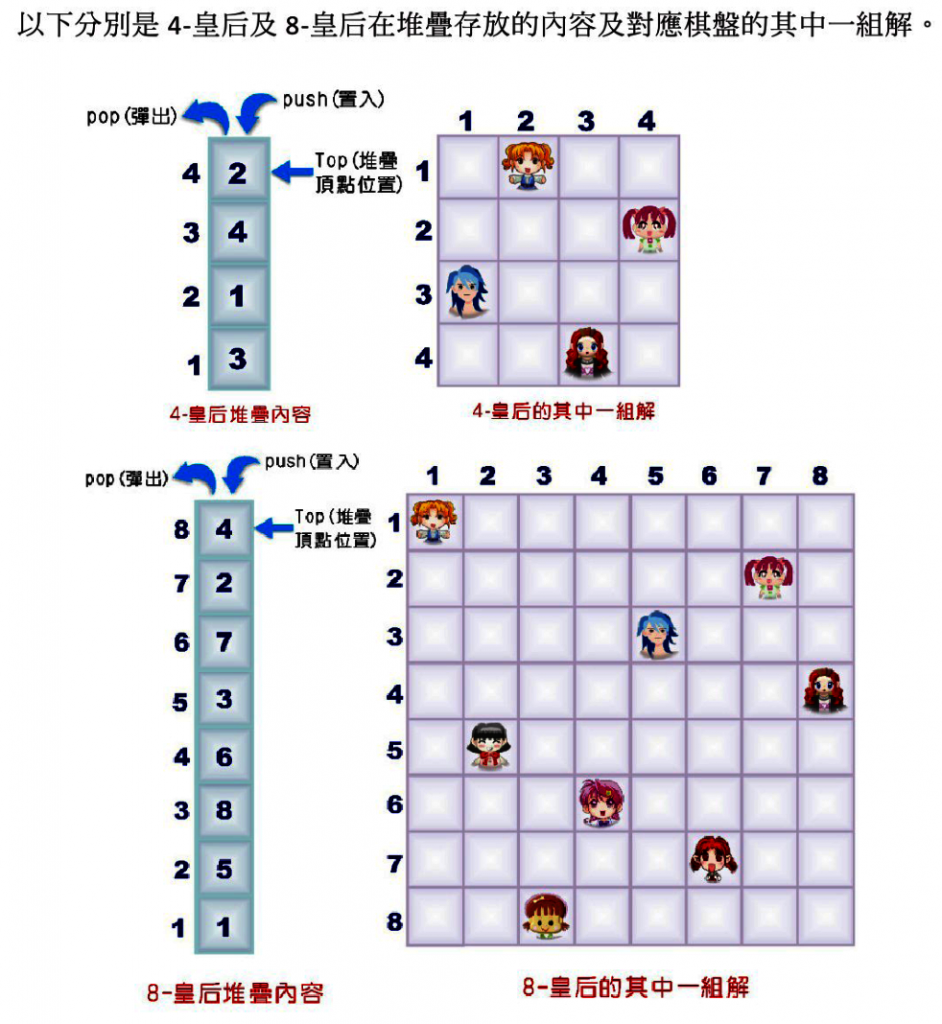
八皇后問題也是一種常見的堆疊應用實例。在西洋棋中的皇后可以在沒有限定一步走幾格的前提下,對其盤中的其他棋子直吃、橫吃及對角斜吃(左斜吃或右斜吃皆可),只要後放入的新皇后,再放入前必須考慮所放置直線方向、橫線方向或對角線方向是否已被放置就皇后,否則就會被先放入的舊皇后吃掉。
利用這個觀念,我們可以將其應用在4*4的棋盤,就稱為4-皇后問題;應用在8*8的棋盤,就稱為8-皇后問題。應用在N*N的棋盤,就稱為N-皇后問題。要解決N-皇后問題(在此我們以8-皇后為例),首先當於棋盤中置入一新皇后,且這個位置不被先前放置的皇后吃掉,則將此新皇后的位置存入堆疊。
但若欲放置新皇后的該行(或該列)的8個位置,都沒有辦法放置新皇后(亦即一放入任何一個位置,就會被先前放置的舊皇后給吃掉)。此時,就必須由堆疊中取出前一個皇后的位置,並於該行(或該列)中重新尋找另一個新的位置放置,在將該位置存入堆疊中,而這種方式就是一種回溯Backtracking)演算法的應用概念。
N-皇后問題的解答,就是配合堆疊及回溯兩種演算概念,以逐行(或逐列)找新皇后位置(如果找不到,則回溯到前一行找尋前一個皇后另一個新位置,以此類推)的方式,來尋找N-皇后問題的其中一組解答。
JS queen.js
程式碼:如下
const EIGHT=8; //定義最大堆疊容量
queen = []; //存放8個皇后之列位
number=0; //計算總共幾組解的總數
//決定皇后存放的位置
//輸出所需要的結果
var print_table=()=> {
let x=y=0;
number+=1;
process.stdout.write('\n');
process.stdout.write('八皇后問題的第'+number+'組解\n\t');
for (x=0; x<EIGHT ; x++) {
for (y=0; y<EIGHT ; y++){
if (x==queen[y])
process.stdout.write('<q>');
else
process.stdout.write('<->');
}
process.stdout.write('\n\t');
}
}
//測試在(row,col)上的皇后是否遭受攻擊
//若遭受攻擊則傳回值為1,否則傳回0
var attack=(row, col)=>{
let i=0;
atk=false;
offset_row=offset_col=0;
while ((atk!=1) && i<col) {
offset_col=Math.abs(i-col);
offset_row=Math.abs(queen[i]-row);
//判斷兩皇后是否在同一對角線上
if ((queen[i]==row || offset_row==offset_col))
atk=true;
i=i+1;
}
return atk;
}
var decide_position=(value)=>{
let i=0;
while (i<8) {
//是否受到攻擊攻擊判斷式
if (attack(i,value)!=1) {
queen[value]=i;
if (value==7)
print_table();
else
decide_position(value+1);
}
i++;
}
}
//主程式
decide_position(0);
6-5 陣列實作佇列
以陣列結構來製作佇列的好處是演算法相當簡單,不過與堆疊不同之處是需要擁有兩種基本動作加入與刪除,而且使用frint與rear兩個註標來分別指向佇列的前端與尾端,缺點是陣列大小並無法事先規劃宣告。首先我們需要宣告一個有限容量的陣列,並以下列說明:
const MAXSIZE=4;
queue=[]; //佇列大小為4
front=-1;
rear=-1;

JS array_queue.js
const MAX=10; //定義佇列的大小
queue=[];
var front=rear=-1;
var choice='';
const prompt = require ('prompt-sync')();
while (rear<MAX-1 && choice !='e') {
const choice = prompt('[a]表示存入一個數值[d]表示取出一個數值[e]表示跳出此程式: ');
if (choice=='a') {
const val = parseInt(prompt('[請輸入數值]: '));
rear+=1;
queue[rear]=val;
}
else if (choice=='d') {
if (rear>front) {
front+=1;
process.stdout.write('[取出數值為]: ' +queue[front]+'\n');
queue[front]=0;
}
else{
process.stdout.write('[佇列已經空了]\n');
return;
}
}
else {
process.stdout.write('\n');
break;
}
}
process.stdout.write('---------------------------\n');
process.stdout.write('[輸出佇列中所有元素]: \n');
if (rear==MAX-1)
process.stdout.write('[佇列已滿]\n');
else if (front>=rear) {
process.stdout.write('沒有\n');
process.stdout.write('[佇列已空]\n');
}
else {
while (rear>front) {
front+=1;
process.stdout.write('['+queue[front]+'] ');
}
process.stdout.write('\n');
process.stdout.write('---------------------------------------------\n');
}
process.stdout.write('\n');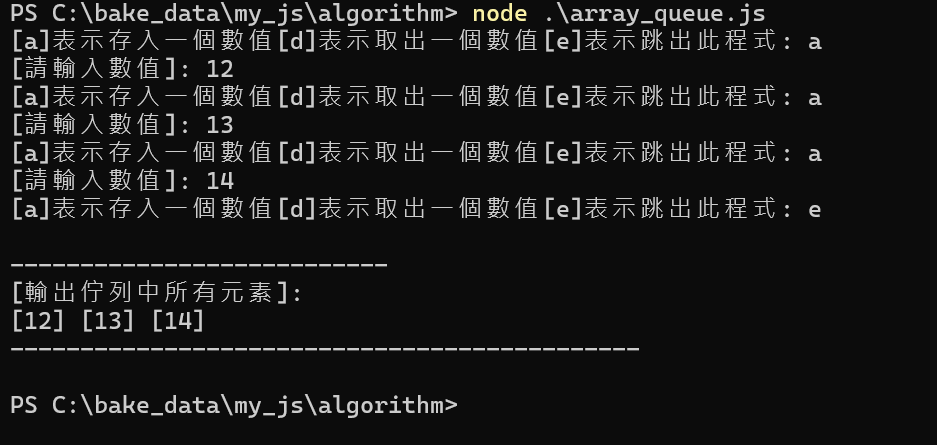
PHP array_queue.php
$choice="n";
$queue=$_SESSION['queue'];
$length = length($queue);
if($_GET['choice'])
$choice=$_GET['choice'];
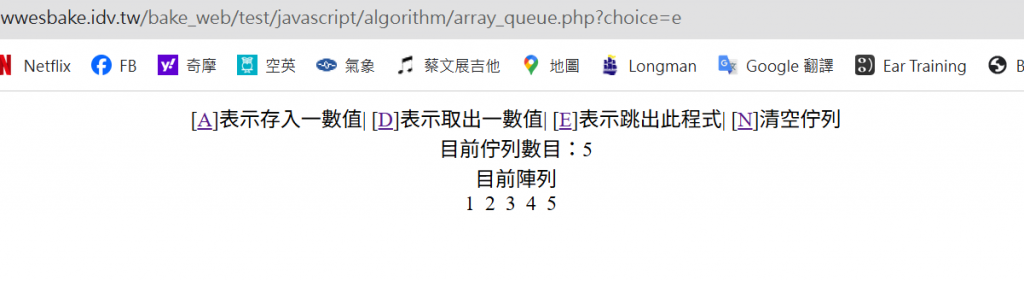
echo "<center>[<a href=".$_SERVER['PHP_SELF']."?choice=a>A</a>]表示存入一數值|
[<a href=".$_SERVER['PHP_SELF']."?choice=d>D</a>]表示取出一數值|
[<a href=".$_SERVER['PHP_SELF']."?choice=e>E</a>]表示跳出此程式|
[<a href=".$_SERVER['PHP_SELF']."?choice=n>N</a>]清空佇列
</center>";
if($choice)
switch ($choice){
case 'a':
echo "
<center>
<form method='post' action={$_SERVER['[PHP_SELF]']}>
請輸入數值:
<input name='add_queue' type='text'>
<input type='submit' name='submit' value='送出''>
</form>
</center>
";
break;
case 'd':
$queue=$_SESSION['queue']; //取出
$del=$queue[0];
array_shift($queue);
echo "<center> 刪除 {$del} </center>";
$_SESSION['queue']=$queue; //存入
break;
case 'e':
//$length = length($queue);
echo "
<center>目前佇列數目:{$length}</center>
";
break;
case 'n':
unset($_SESSION['queue']);
session_destroy();
break;
}
if ($_POST['submit']=='送出'){
//echo $_POST['add_queue'];
$queue=array(); //先宣告陣列
//print_r($queue)."<br>";
//print_r($_SESSION['queue'])."<br>";
$queue = $_SESSION['queue']; //取出
//array_push ($queue, $_POST['add_queue']); //不知為什麼會出現錯誤,但是queue有值後就不會出現
$queue[]=$_POST['add_queue']; //加入陣列
$_SESSION['queue']=$queue; //存入
}
echo "<center>目前陣列"."<br>";
//print_r($queue);
//echo "here";
foreach ($_SESSION['queue'] as $value){
echo $value." ";
}
function length ($arr){
return count($arr);
} $queue=array();
$queue = $_SESSION['queue']; //取出
$queue[]=$_POST['add_queue']; //加入陣列
可以改寫為
$_SESSION['queue'][]=$_POST['add_queue'];