
全方位應用的陣列與串列演算法
5-1-1矩陣相加
請設計一程式來宣告3個二維陣列,來實作2個矩陣相加的過程,並顯示兩矩陣相加後的結果。
JS matrix_add.js
var A = new Array();
var B = new Array();
var C = new Array();
for (let i=0; i<3; i++){
A[i]=new Array();
B[i]=new Array();
C[i]=new Array();
}
A= [[1,3,5],[7,9,11],[13,15,17]];
B= [[9,8,7],[6,5,4],[3,2,1]];
N=3;
for (let i=0;i<3; i++){
for (let j=0; j<3; j++){
C[i][j]=A[i][j]+B[i][j];
}
}
console.log("[矩陣A和矩陣B相加的結果]");
let str='';
for (let i=0; i<3; i++){
for (let j=0; j<3; j++){
str=str+C[i][j]+'\t';
}
str=str+'\n';
}
console.log(str);PHP matrix_add.php
$A_arr=array(array(1,3,5),array(7,9,11),array(13,15,17));
$B_arr=array(array(9,8,7),array(6,5,4),array(3,2,1));
$C_arr=array();
for ($i=0; $i<count($A_arr); $i++){
for($j=0; $j<count($A_arr);$j++){
$C_arr[$i][$j] = $A_arr[$i][$j] + $B_arr[$i][$j];
}
}
print_r($C_arr);
echo "<br><hr><br>";
foreach ($C_arr as $item ){
echo "[";
$t=1;
foreach ($item as $value){
if($t<3) echo $value.",";
else echo $value;
$t++;
}
echo "]<br>";
}函式說明
foreach ($arr as $yourstr){
echo $yourstr //$yourstr => $arr or $value
}
5-1-2矩陣相乘
如果談到兩個矩陣A與B的相乘,是有某些條件限制。首先必須符合A為一個m*n的矩陣,B為一個n*p的矩陣,對A*B之後的結果為一個m*p的矩陣C。
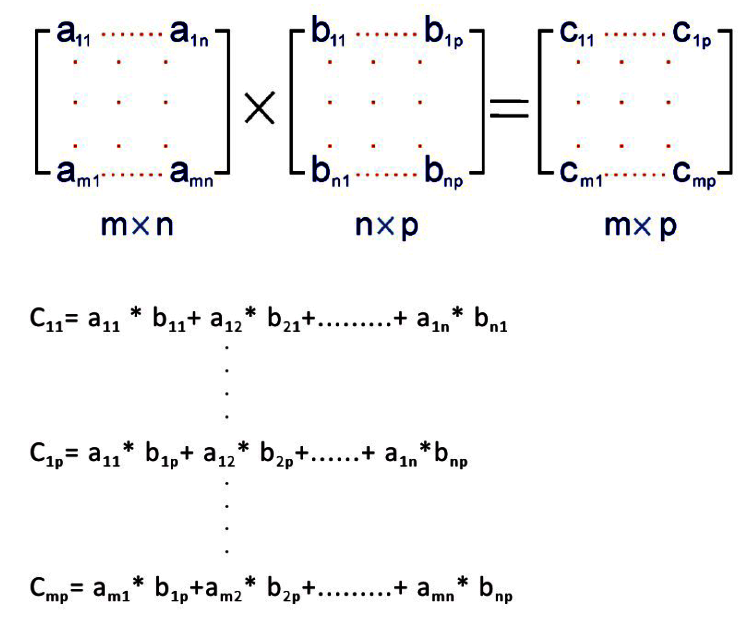
範例:
請設計一程式來實作下列兩個矩陣的相乘結果。
JS matrix_multiply.js
const M=2;
const N=3;
const P=2;
A=[6,3,5,8,9,7];
B=[5,10,14,7,6,8];
C=[0,0,0,0];
if (M<=0 || N<=0 || P<=0) console.log('[錯誤:維數M,N,P必須大於0]');
for (let i=0; i<M; i++){
for (let j=0; j<P; j++){
let Temp=0;
for (let k=0; k<N; k++) Temp = Temp +parseInt(A[i*N+k])*parseInt(B[k*P+j]);
C[i*P+j] = Temp;
}
}
console.log('[AxB的結果是]');
let str='';
for (i=0; i<M; i++){
for (j=0; j<P; j++){
str = str+C[i*P+j]+ '\t';
}
str = str+'\n';
}
console.log(str);PHP matrix_multiply.php
$a_arr = array(array(6,3,5),array(8,9,7));
$b_arr = array(array(5,10),array(14,7),array(6,8));
$a_m = count($a_arr); //陣列 M列
$a_n = count($a_arr[0]); //陣列 N行
$b_n = count($b_arr); //陣列 N列
$b_p = count($b_arr[0]); //陣列 P行
$c_arr = array();
if ($a_m <=0 || $a_n <=0 || $b_n<=0 || $b_p<=0 || $a_n!=$b_n){
echo "條件錯誤";
}
//echo "a_m=".$a_m."; a_n=".$a_n."<br>";
//echo "b_n=".$b_n."; b_p=".$b_p."<br>";
for ($i=0 ; $i<$a_m; $i++){
for ($j=0; $j<$b_p; $j++){
$temp=0;
for ($k=0 ; $k<$a_n; $k++){
$temp = $temp + intval($a_arr[$i][$k])*intval($b_arr[$k][$j]);
//echo $temp."<br>";
$c_arr[$i][$j]=$temp;
}
//echo $temp."<br>";
}
//echo "--<br>";
}
print_r($c_arr);5-1-3轉置矩陣
「轉置矩陣」At就是把原矩陣的行座標元素相互調換,假設At為A的轉置矩陣,則有At[j,i]=[i,j],如下圖所示:
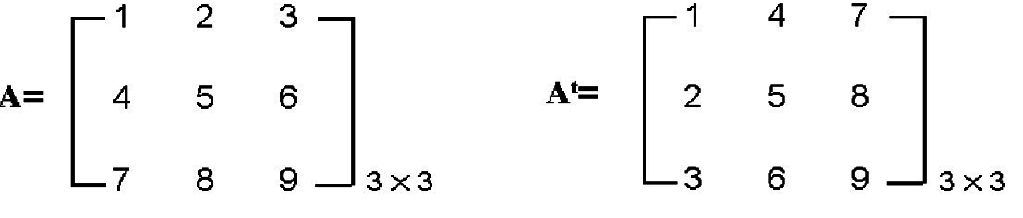
範例
請設計一程式來實作一4*4二微陣列的轉置矩陣。
JS transpose.js
arrA=[[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]];
N=4;
arrB=[[],[],[],[]];
console.log('原設定的矩陣內容');
for (i=0; i<4; i++){
str = '';
for (j=0; j<4; j++){
str= str+arrA[i][j]+'\t';
}
console.log(str);
}
for(i=0; i<4; i++){
for(j=0; j<4; j++){
arrB[i][j]=arrA[j][i];
}
}
console.log('[轉置矩陣的內容為]');
for (i=0; i<4; i++){
str = '';
for (j=0; j<4; j++){
str= str+arrB[i][j]+'\t';
}
console.log(str);
}PHP transpose.php
$a_arr = array(array(1,2,3,4),array(5,6,7,8),array(9,10,11,12),array(13,14,15,16));
$b_arr = array();
$arr_m = count($a_arr);
$arr_n = count($a_arr[0]);
echo "M-".$arr_m."N-".$arr_n."<br>";
for ($i=0; $i<$arr_m; $i++){
for($j=0; $j<$arr_n; $j++){
$b_arr[$i][$j]=$a_arr[$j][$i];
}
}
foreach($a_arr as $item){
foreach ($item as $value){
echo $value." ";
}
echo "<br>";
}
foreach($b_arr as $item){
foreach ($item as $value){
echo $value." ";
}
echo "<br>";
}5-1-4 稀疏矩陣
稀疏矩陣最簡單的定義就是一個矩陣中大部分的元素為0,即可稱為「稀疏矩陣」Sparse Matrix。例如下列的矩陣就是典型的稀疏矩陣。
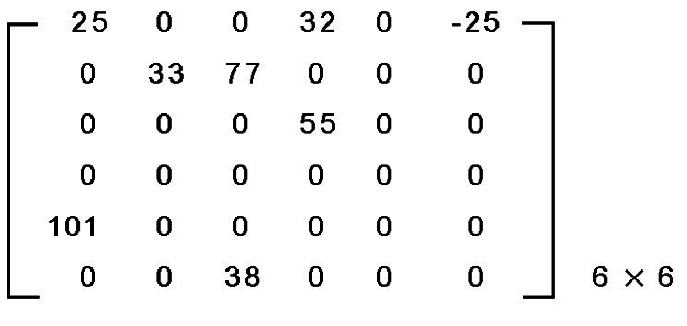
當然如果直接使用傳統的二維陣列來儲存上圖的稀疏矩陣也是可以,但事實上許多元素都是0。這樣的做法在矩陣很大時的稀疏矩陣,就會十分浪費記憶體空間。而改進空間的方法就是利用三項式(3-tuple)的資料結構。我們把每一個非零項目以(i,j,item-value)來表示。更詳細的形容,就是假如一個稀疏矩陣有n個非零項目,那麼可以利用一個A(0:n,1:3)的二維陣列來表示。
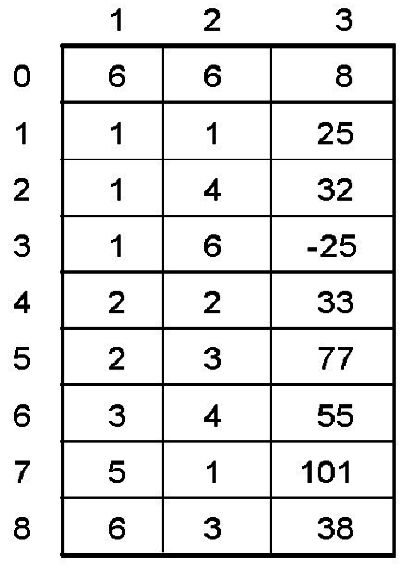
其中A(0,1)代表此稀疏矩陣的列數,A(0,2)代表此稀疏矩陣的行數,而A(0,3)則是此稀疏矩陣非零項目的總數。另外每一個非零項目以(i,j,item-value)來表示。其中i為此非零項目所在的列數,j為此非零項目所在行數,item-value則此分零項的值。以上圖6*6稀疏矩陣為例,則可以以下表示:
A(0,1)=>表示此舉矩陣的列數。
A(0,2)=>表示此舉矩陣的行數。
A(0,3)=>表示此舉矩陣非零項目的總數。
這種利用3項式(3-tuple)資料結構來壓縮稀疏矩陣,可以減少記憶體不必要的浪費。
JS sparse.js
var NONZERO=0;
temp=1;
Sparse=[[15,0,0,22,0,-15],[0,11,3,0,0,0],
[0,0,0,-6,0,0],[0,0,0,0,0,0],
[91,0,0,0,0,0],[0,0,28,0,0,0]];//宣告稀疏矩陣,稀疏矩陣的所有元素設為0
str='';
console.log('[稀疏矩陣的各個元素]');
for (i=0;i<6;i++) {
for(j=0;j<6;j++){
process.stdout.write(Sparse[i][j]+'\t');
if (Sparse[i][j]!=0) NONZERO=NONZERO+1;
}
console.log();
}
Compress=new Array(); //宣告壓縮陣列
for (let i=0; i<NONZERO+1; i++) Compress[i]=[];
//開始壓縮稀疏矩陣
Compress[0][0]=6;
Compress[0][1]=6;
Compress[0][2]= NONZERO;
for (i=0; i<6; i++){
for (j=0; j<6; j++){
if (Sparse[i][j]!=0){
Compress[temp][0]=i;
Compress[temp][1]=j;
Compress[temp][2]=Sparse[i][j];
temp=temp+1;
}
}
}
console.log('[稀疏矩陣壓縮後的內容]');//印出壓縮矩陣
for (i=0; i<NONZERO+1;i++){
for (j=0; j<3; j++){
process.stdout.write(Compress[i][j]+'\t');
}
console.log();
}PHP sparse.php
$sparse=array(array(15,0,0,22,0,-15),array(0,11,3,0,0,0),
array(0,0,0,-6,0,0),array(0,0,0,0,0,0,0),
array(91,0,0,0,0,0),array(0,0,28,0,0,0));
$M = count($sparse);
$N = count($sparse[0]);
$nonzero=0;//計算沒有為零的數量
$temp=1;
$compress=array();
for ($i=0; $i<$N; $i++){
for($j=0; $j<$N; $j++){
if ($sparse[$i][$j]!=0)
$nonzero=$nonzero+1;
}
}
echo "原始陣列"."<br>";
foreach ($sparse as $key => $item) {
foreach($item as $list => $value){
echo $value." ";
}
echo "<br>";
}
$compress[0][0]=$M;
$compress[0][1]=$N;
$compress[0][2]=$nonzero;
for($i=0; $i<$N; $i++){
for($j=0; $j<$M; $j++){
if ($sparse[$i][$j]!=0){
$compress[$temp][0]=$i;
$compress[$temp][1]=$j;
$compress[$temp][2]=$sparse[$i][$j];
$temp=$temp+1;
}
}
}
echo "壓縮後的陣列<br>";
foreach ($compress as $key => $item) {
foreach($item as $list => $value){
echo $value." ";
}
echo "<br>";
}