
9-2鏈結串列實作二元樹
所謂鏈結串列實作二元樹,就是利用鏈結串列來儲存二元樹。基本上,使用串列來表示二元樹的好處是對於節點的增加與刪除相當容易,缺點是很難找到父節點,除非在每一節點多增加一個欄位。以上述宣告而言,此節點所存放的資料型態為整數。寫成如下宣告:
class tree {
constructor() {
this.data=0;
this.left=null;
this.right=null;
}
}
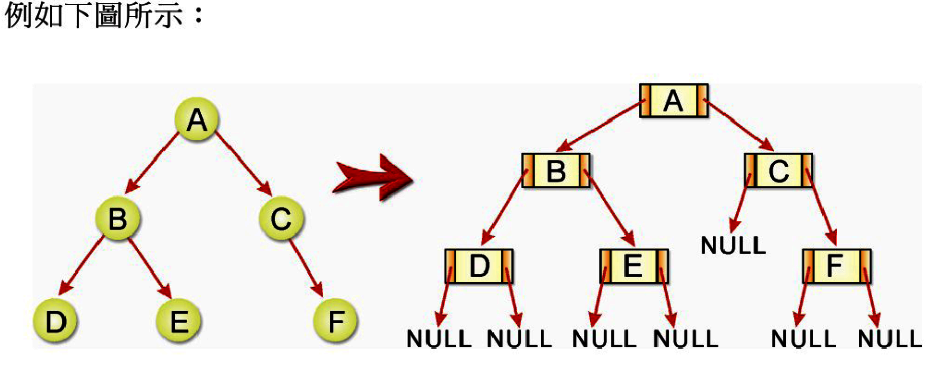
以串列方式建立二元樹的演算法如下:
var creat_tree=(root,val)=> {
newnode=new tree();
newnode.data=val;
newnode.left=null;
newnode.right=null;
if (root==null) {
root=newnode;
return root;
}
else {
current=root;
while (current!=null) {
back=current;
if (current.data>val)
current=current.left;
else
current=current.right;
}
if (back.data>val)
backup.left=newnode;
else
backup.right=newnode;
}
return root;
}

JS list_tree.js
class tree {
constructor() {
this.data=0;
this.left=null;
this.right=null;
}
}
var create_tree=(root,val)=> {
newnode=new tree();
newnode.data=val;
newnode.left=null;
newnode.right=null;
if (root==null) {
root=newnode;
return root;
}
else {
current=root;
while (current!=null) {
backup=current;
if (current.data>val)
current=current.left;
else
current=current.right;
}
if (backup.data>val)
backup.left=newnode;
else
backup.right=newnode;
}
return root;
}
data=[5,6,24,8,12,3,17,1,9];
ptr=null;
root=null;
for (i=0; i<9; i++)
ptr=create_tree(ptr,data[i]);
process.stdout.write('左子樹:\n');
root=ptr.left;
while (root!=null) {
process.stdout.write(root.data+'\n');
root=root.left;
}
process.stdout.write('------------------------------\n');
process.stdout.write('右子樹:\n');
root=ptr.right;
while (root!=null) {
process.stdout.write(root.data+'\n');
root=root.right;
}
process.stdout.write('\n');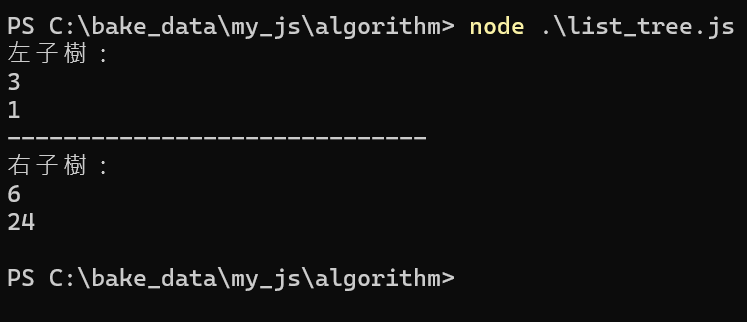
PHP list_tree.php
class Node {
public $data;
public $left;
public $right;
public function __construct($data) {
$this->data = $data;
$this->left = null;
$this->right = null;
}
}
// 定義二元搜尋樹類別
class BinaryTree {
public $root;
public function __construct() {
$this->root = null;
}
// 插入節點(遞迴方式)
public function insert($data) {
$this->root = $this->insertRecursively($this->root, $data);
}
private function insertRecursively($node, $data) {
if ($node === null) {
return new Node($data);
}
if ($data < $node->data) {
$node->left = $this->insertRecursively($node->left, $data);
} else {
$node->right = $this->insertRecursively($node->right, $data);
}
return $node;
}
// 中序遍歷(in-order traversal)
public function inorderTraversal($node) {
if ($node !== null) {
$this->inorderTraversal($node->left);
echo $node->data . " ";
$this->inorderTraversal($node->right);
}
}
}
// 使用範例
$tree = new BinaryTree();
$tree->insert(50);
$tree->insert(30);
$tree->insert(70);
$tree->insert(20);
$tree->insert(40);
$tree->insert(60);
$tree->insert(80);
echo "中序遍歷結果: ";
$tree->inorderTraversal($tree->root);PHP create_tree.php
用class實作二元數:目前中序走訪函數有問題
改為另一個PHP解法 create_tree-1.php
class TreeNode {
public $value;
public $left;
public $right;
public function __construct($value) {
$this->value = $value;
$this->left = null;
$this->right = null;
}
}
function insertBST($root, $value) {
if ($root === null) {
return new TreeNode($value);
}
if ($value < $root->value) {
$root->left = insertBST($root->left, $value);
} else {
$root->right = insertBST($root->right, $value);
}
return $root;
}
// 測試:建 BST
$values = [10, 5, 15, 3, 7, 12, 18];
$root = null;
foreach ($values as $val) {
$root = insertBST($root, $val);
}
// 中序遍歷 BST
function inorderTraversal($node) {
if ($node === null) return;
inorderTraversal($node->left);
echo $node->value . ' ';
inorderTraversal($node->right);
}
inorderTraversal($root); // 輸出:3 5 7 10 12 15 18