圖形演算法的關鍵課程
圖形除了被活用在演算法領域中最短路徑搜尋、拓樸排序外,還能應用在系統分析中以時間為評核標準的計畫平核術(Performance Evaluation and Review Technique, PERT),或者像一般生活中的(IC版設計)、(交通網路規劃)等都可以看作是圖形的應用。利用兩點之間的距離,如何計算兩節點之間最短距離,就變成圖形要處理的問題,也就是網路的定義,以Dijkstra 這種圖形演算法就能快速尋找出兩個節點之間的最短路徑,如果沒有Dijkstra 演算法,現在網路的運作效率必將大大降低。
圖形理論起源1736年,一位瑞士數學家尤拉(Euler)為了解決(肯尼茲堡橋梁)問題,所想出來的一種資料結構理論,就是著名的七橋理論。簡單來說,就是有七座橋橫跨四個城市的大橋。尤拉索思考的問題是這樣的,(是否有人在只經過每一座橋梁一次的情況下,把所有地方走過一次而且回到原點。)
10-1-1尤拉環與尤拉鏈
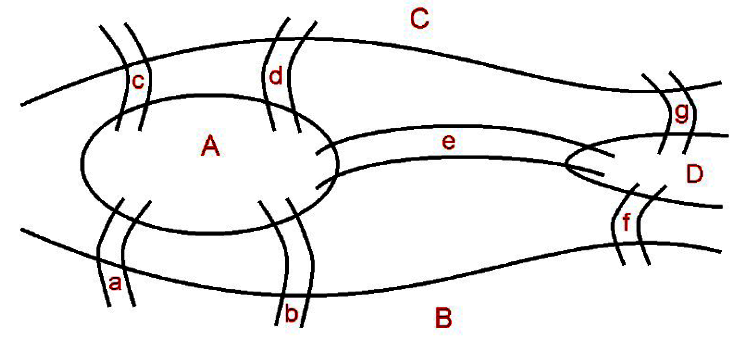
尤拉當時使用的方法就是以圖形結構進行分析。他先以頂點表示土地,以邊表示橋梁,並定義連接每個頂點的邊數稱為該頂點的分支度。我們將以下面簡圖來表示(肯尼茲堡橋梁)問題。
最後尤拉找到一個結論:(當所有頂點的分支度皆為偶數時,才能從某頂點出發,經過每一邊一次,再回到起點。)也就是說,在上圖中每個頂點的分支度都是奇數,所以尤拉所思考的問題是不可能發生的,這個理論就是有名的(尤拉環)(Eulerian cycle)理論。
但如果條件改成從某頂點出發,經過每邊一次,不一定要回到起點,亦即只允許其中兩個頂點的分支度是奇數,其餘則必須全部為偶數,符合這樣的結果稱為尤拉鏈(Eulerian chain)。
10-1-2圖形的定義
圖形是由(頂點)和(邊)所組成的集合,通常用G=(V,E)來表示,其中V是所有頂點的集合,而E代表所有的集合。圖形的種類有兩種:一是無向圖形,一是有向圖形,無向圖形以(V1,V2)表示,有向圖形則以<V1,V2>表示其邊緣。
10-1-3無向圖形
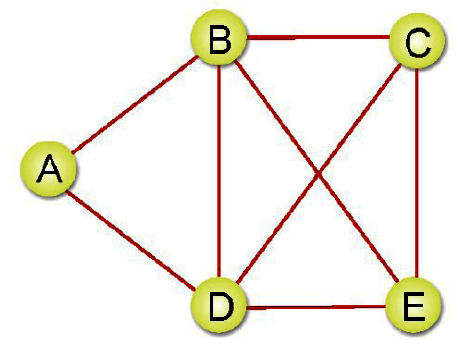
無向圖形(Graph)是一種具備同邊的兩個項點沒有次序關係,例如(A,B)與(B,A)是代表相同的邊。如下圖所示:
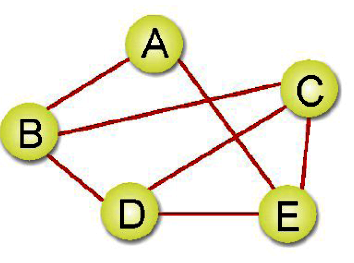
V={A,B,C,D,E}
E={(A,B),(A,E),(B,C),(B,D),(C,D),(C,E),(D,E)}
接下來是無向圖形的重要術語介紹:
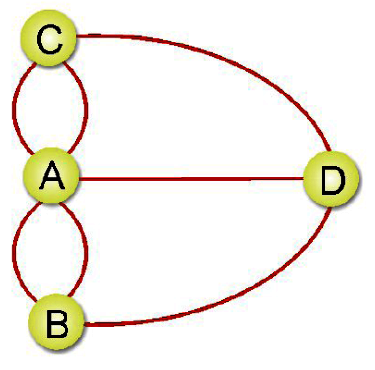
完整圖形:在(無向圖形)中,N個頂點正好有N(N-1)/2條邊,則稱為(完整圖形)。如下圖
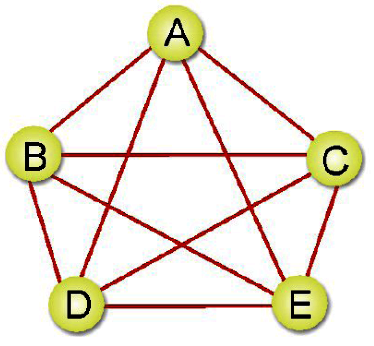
路徑(PATH):對於從頂點Vi到頂點Vj的一條路徑,是由所經過頂點所成的連續數列,如上圖G中,A到E的路徑有{(A,B)、(B,E)}及{(A,B)、(B,C)、(C,D)、(D,E)}等等。
簡單路徑(Simple Path):除了起點和終點可能相同外,其他經過的頂點都不同,在圖G中,(A,B)、(B,C)、(C,A)、(A,E)不是一條簡單路徑。
路徑長度(Path Length):是指路徑上所包含的數目,在圖G中,(A,B)、(B,C)、(C,D)、(D,E),是一條路徑,其長度為4,且為一簡單路徑。
循環(Cycle):起始頂點及終止頂點為同一個點的簡單路徑稱為循環。如上圖G,{(A,B)、(B,D)、(D,E)、(E,C)、(C,A)}起點及終點都是A,所以是一個循環。
依附(Incident):如果Vi與Vj相鄰,我們則稱(Vi,Vj)這邊依附於頂點Vi及頂點Vj,或者依附於頂點B的邊有(A,B)、(B,D)、(B,E)、(B,C)。
子圖(Subgraoh):當我們稱G’為G的子圖時,必定存在V(G’)<=V(G)與E(G’)<=E(G),如下圖是上圖G的子圖。
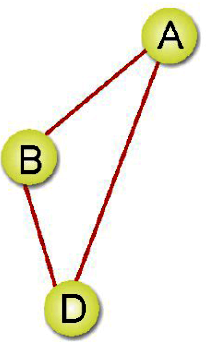
相鄰(Adjacent):如果(Vi,Vj)是E(G)中的一邊,則稱Vi與Vj相鄰。
相連單元(Connected Component):在無向圖形中,相連在一起的最大子圖(Subgraph),如下圖有2個相連單位。
分支度:在無向圖形中,一個頂點所擁有邊的總數為分支度。如上圖G,頂點A的分支度為4。