10-2-2相鄰串列法
前面所介紹相鄰矩陣法,優點是藉著矩陣的運算,可以求取許多特別的應用,如要在圖形中加入新邊時,這個表示法的插入與刪除相當簡易。不過可慮到稀疏矩陣空間浪費的問題,如要計算所有頂點的分支度時,其時間複雜度為O(n^2)。
因此可以考慮更有效率的方法,就是相鄰串列法(adjaceny list)。這種表示法就是將一個n列相鄰矩陣,表示成n個鏈結串列,這種做法和相鄰矩陣相比較節省空間,如計算所有頂點的分支度時,其時間複雜度為O(n+e),缺點是圖形新邊的加入或刪除會更動到相關的串列鏈結,較為麻煩費時。
首先將圖形的n個頂點形成n個串列首,每個串列中的節點表示它們和首節點之間有邊相連。節點宣告如下:
class list_node {
constructor () {
this.val=0;
this.next=null;
}
}
在無向圖形中,因為對稱的關係,若有n個頂點、m個邊,則形成n個串列首,2m個節點。若為有向圖形中,則有n個串列首,以及m個頂點,因此相鄰串列中,求所有頂點分枝度所需的時間複雜度為O(n+m)。現在分別來討論下圖中兩個範例,該如何使用相鄰串列表示:
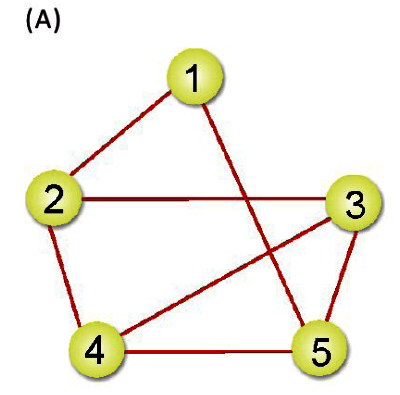
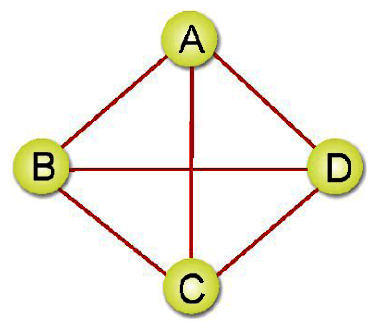
首先來看(A)圖,因為5個頂點使用5個串列首,V1串列代表頂點1,與頂點1相鄰的頂點有2及5,依此類推。
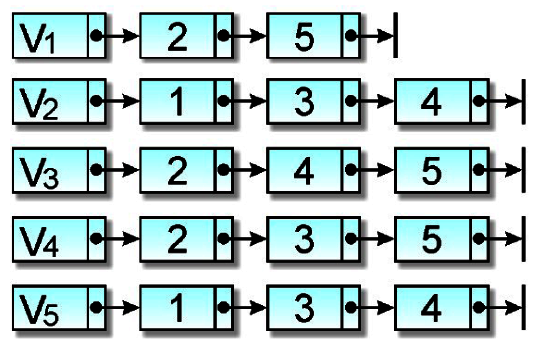
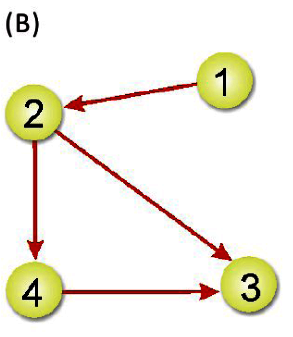
接著來看(B)圖,因為4個頂點使用4個串列首,V1串列代表頂點1,與頂點1相鄰的頂點有2,依此類推。

JS adjaceeency_matrix.js
class list_node {
construnctor() {
this.val=0;
this.next=null;
}
}
head=[];
for (i=0; i<6; i++) {
head[i]=new list_node();
}
var newnode=new list_node();
//圖形宣告
data=[[1,2],[2,1],[2,5],[5,2],
[2,3],[3,2],[2,4],[4,2],
[3,4],[4,3],[3,5],[5,3],
[4,5],[5,4]];
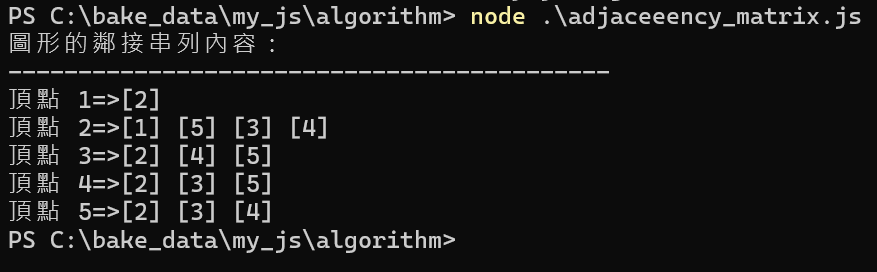
process.stdout.write('圖形的鄰接串列內容:\n');
process.stdout.write('-------------------------------------------\n');
for (i=1; i<6; i++) {
head[i].val=i;
head[i].next=null;
process.stdout.write('頂點 '+i+'=>');
ptr=head[i];
for (j=0; j<14; j++) {
if (data[j][0]==i) {
newnode.val=data[j][1];
newnode.next=null;
while (ptr!=null) ptr=ptr.next;
ptr=newnode;
process.stdout.write('['+newnode.val+'] ');
}
}
process.stdout.write('\n');
}
PHP adjacency_matrix.php
PHP的串列,不會寫。
搞不清楚 javascript newnode.val 跟 newnode.next如何改寫成PHP。
10-2-3 相鄰複合串列法
上面介紹了兩個圖形表示法都是從頂點的觀點出發,但如果要處理的是(邊)則必須使用相鄰多元串列,相鄰多元串列是處理無向圖形的另一種方法。相鄰多元串列的節點是存放邊線的資料,其結構如下:

其中相關特性說明如下:
M:是紀錄該邊是否被找過的一個位元之欄位。
V1及V2:是所記錄的邊的起點與終點。
LINK1:在尚有其他頂點與V1相連的情況下,此欄位會指向下一個與V1相連的邊結點,如果已經沒有任何頂點與V1相連時,則指向null。
LINK2:在尚有其他頂點與V2相連的情況下,此欄位會指向下一個與V2相連的邊節點,如果已經沒有任何頂點與V2相連時,則指向null。
例如有三條邊線(1,2)(1,3)(2,4),則邊線(1,2)表示法如下:
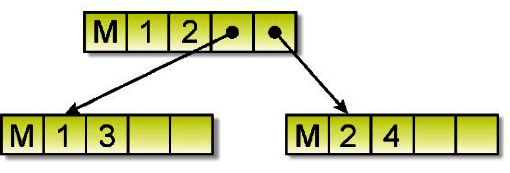
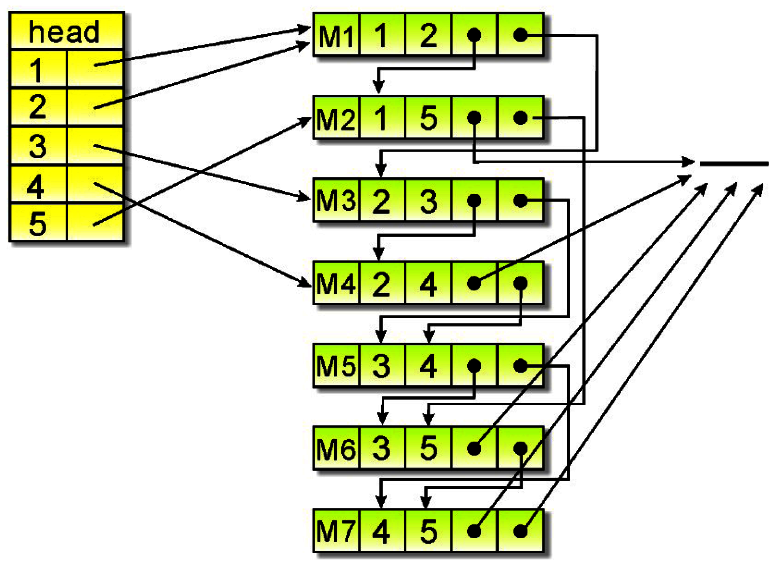
我們現在已相鄰多元串列表示下圖所示:
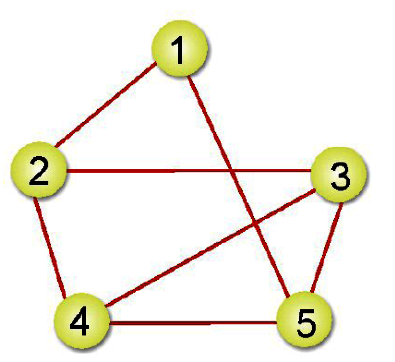
首先分別把頂點及邊的節點找出。
10-2-4 索引表格法
索引表格表示法,是一種用一維陣列來依序儲存與各頂點相鄰的所有頂點,並建立索引表格,來記錄個頂點在此一維陣列中第一個與該頂點相鄰的位置。我們將以下圖來說明索引表格法的實例。

則索引表格法的表示外觀為: