10-4 擴張術的密碼
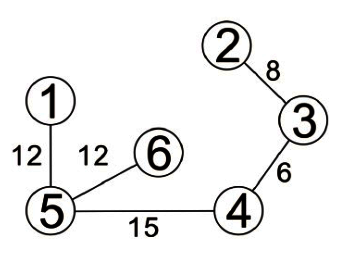
擴張樹又稱(花費樹)或(植樹),一個圖形的擴張樹(Spanning Tree)就是以最少的編來連結圖形中所有的頂點,且不造成循環(Cycle)的樹狀結構。假設在樹的編加上一個權重(weight)值,這種圖形就成為(加權圖形 Weighted Graph)。如果這個權重值代表兩個頂點間的距離(distance)或成本(Cost),這類圖形就稱為網路(Network)。如下圖所示:
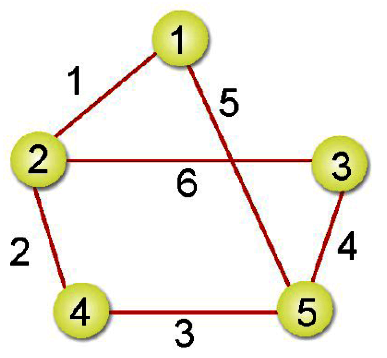
假如想知道從某個點到另一個點間的路徑成本,例如由頂點1到頂點5有(1+2+3)、(1+6+4)及5這三個路徑成本,而(最小成本擴張樹Minimun Cost Spanning Tree)則是路徑成本為5的擴張樹。請看說明:
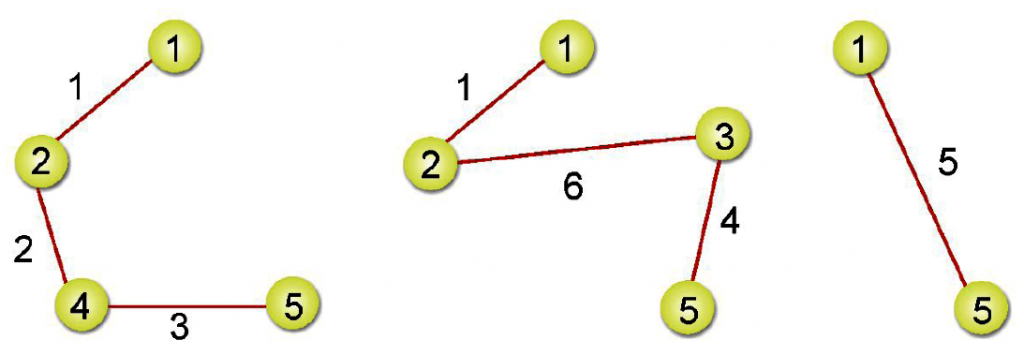
一個加權圖形中如何找到最小成本擴張樹是相當重要,因為許多工作都可以由圖形來表示,例如從高雄到花蓮的距離或花費等。接著將介紹以所謂(貪婪法則Greedy Rule)為基礎,來求得一個無向連通圖形的最小花費樹的常見建立方法。分別是Prim’s演算法及Kruskal’s演算法。
10-4-1 Prim演算法
Prim 演算法又稱P氏法,對一個加權圖形G=(V,E),設V={1,2,……n},假設U={1},也就是說,U及V是兩個頂點的集合。
然後從U-V差集所產生的集合中找出一個頂點x,該頂點x能與U集合中的某點形成最小成本的邊,且不會造成迴圈。然後將頂點x加入U集合中,反覆執行同樣的步驟,一直到U集合等於V集合(即U=V)為止。
接下來,我們將實際利用P氏法求出下圖的做小擴張樹。
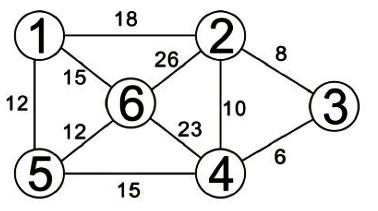
從此圖形中可得V={1,2,3,4,5,6},U=1
從V-U={2,3,4,5,6}中找一頂點與U頂點能形成最小成本邊,得
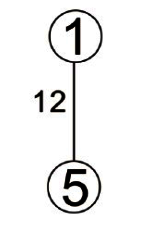
V-U={2,3,4,6} U={1,5}
從V-U中頂點找出與U頂點能形成最小成本的邊,得
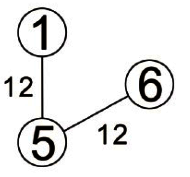
且 U={1,5,6},V-U={2,3,4}
同理,找到頂點4
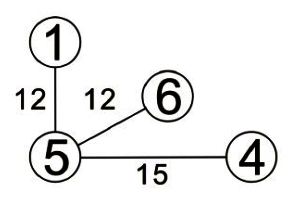
U={1,5,6,4},V-U={2,3}
同理,找到頂點3
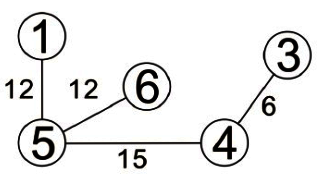
同理,找到頂點2