9-7堆積樹排序法-2
下面我們利用堆積排序法針對34、19、40、14、57、17、4、43的排序過程示範如下:
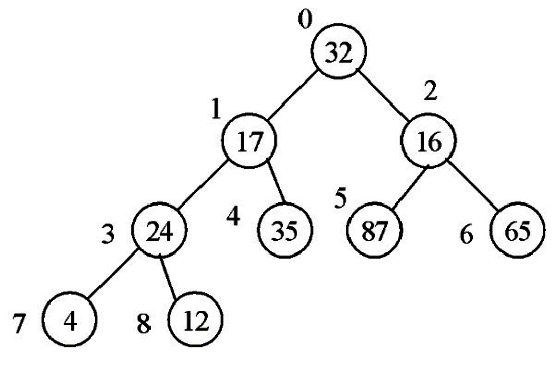
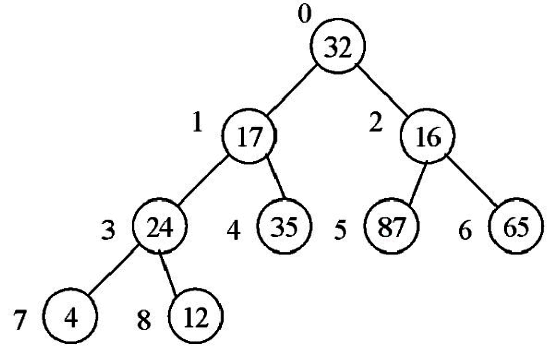
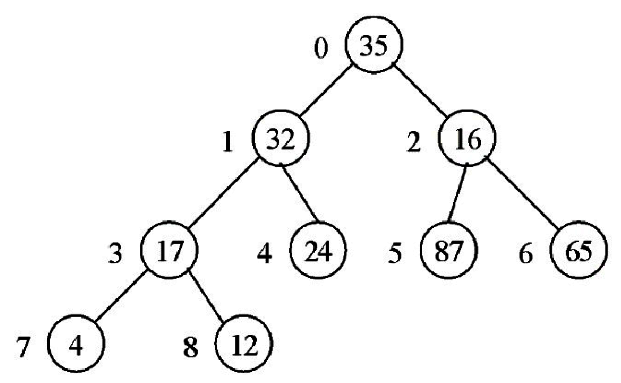
1.依下圖數字順序建立完整二元數。
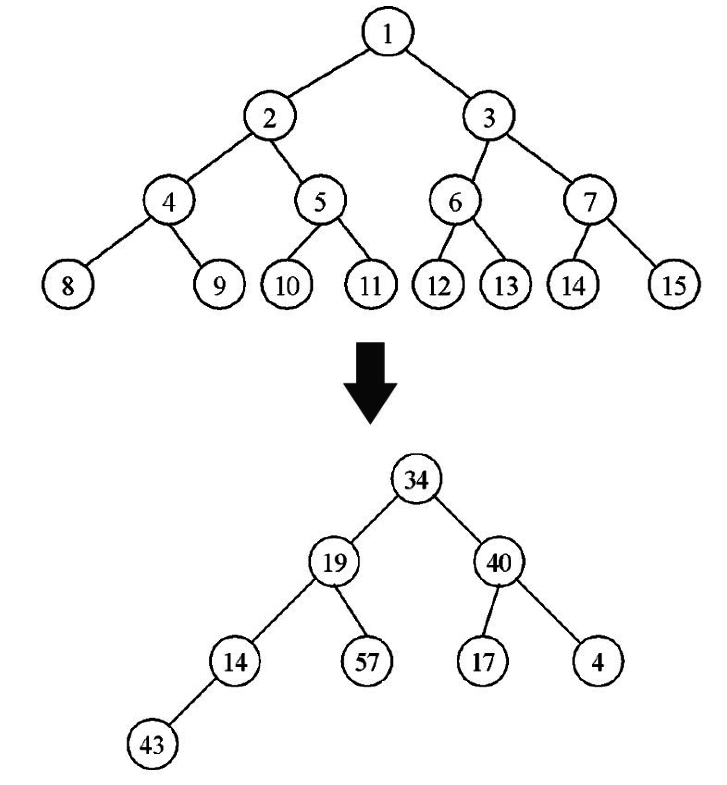
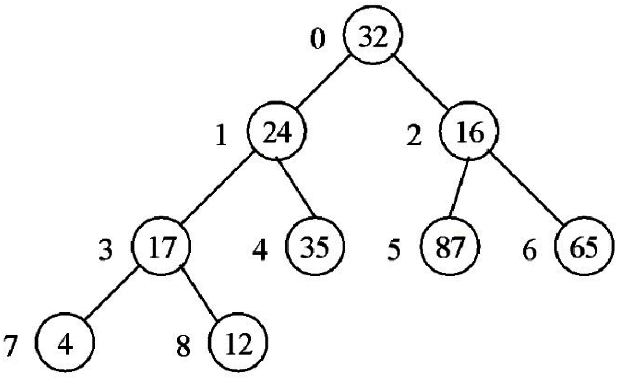
2.建立堆積樹
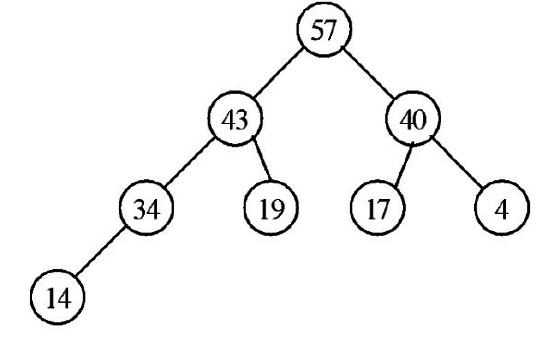
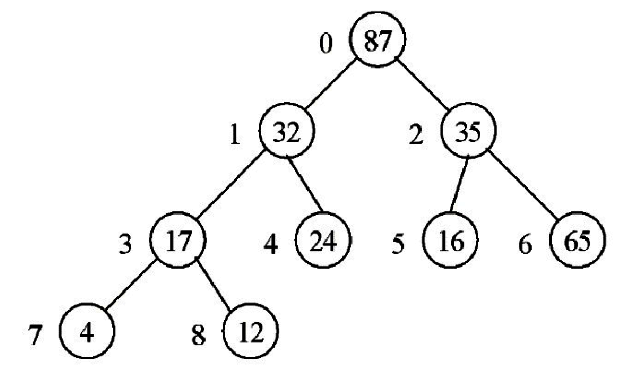
3.將57自樹根移除,重新建立堆積樹
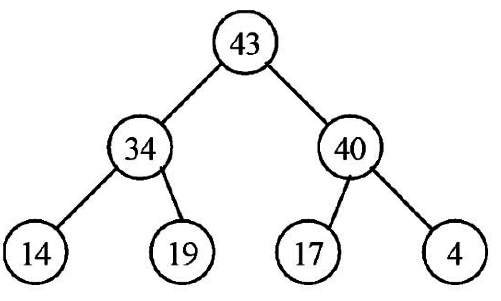
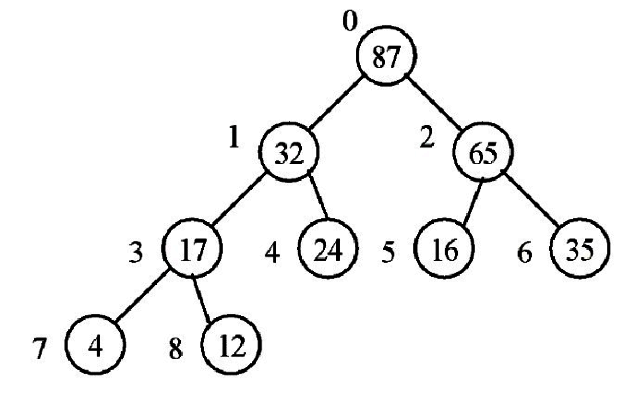
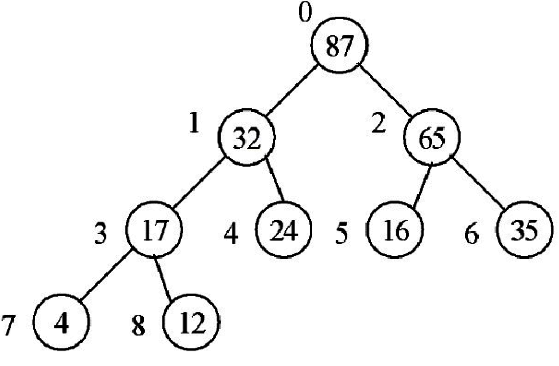
4.將43自樹根移除,重新建立堆積樹。
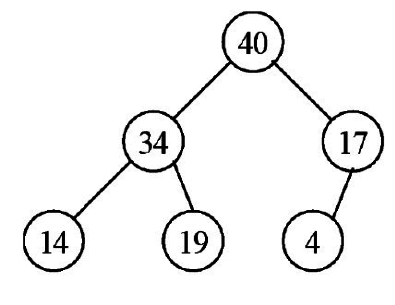
5.將40樹根移除,重新建立堆積樹

6.將34自樹根移除,重新建立堆積樹
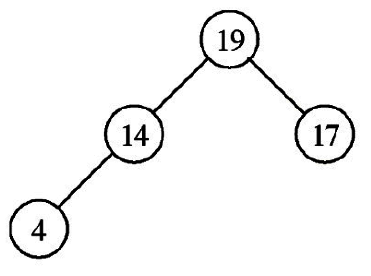
7.將19自樹根移除,重新建立堆積樹
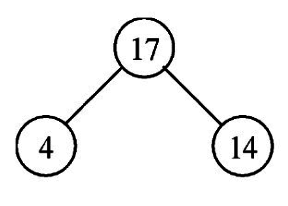
8.將17自樹根移除,重新建立堆積樹
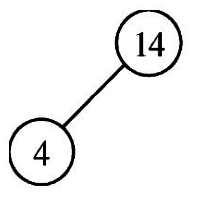
9.將14自樹根移除,重新建立堆積樹

最後將4自樹根移除。得到的排序結果為57、43、40、34、19、17、14、4
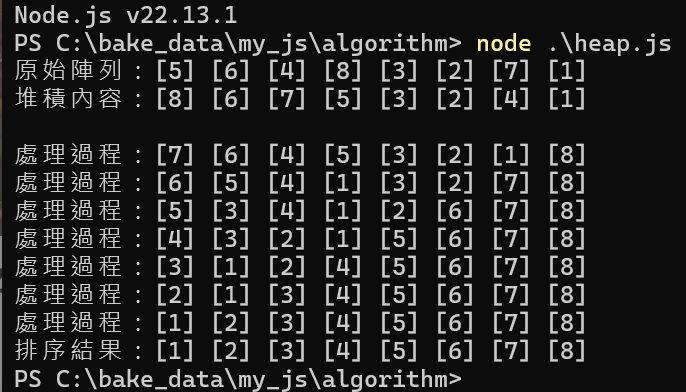
JS heap.js
var heap=(data,size)=> {
for (let i=Math.floor(size/2); i>0; i--)
ad_heap(data, i, size-1);
process.stdout.write('\n');
process.stdout.write('堆積內容:');
for (let i=1; i<size; i++)
process.stdout.write('['+data[i]+'] ');
process.stdout.write('\n\n');
for (let i=size-2; i>0; i--) {
temp=data[1];
data[1]=data[i+1];
data[i+1]=temp;
ad_heap(data, 1, i);
process.stdout.write('處理過程:');
for (let j=1; j<size; j++)
process.stdout.write('['+data[j]+'] ');
process.stdout.write('\n');
}
}
var ad_heap=(data, i, size)=> {
j=2*i;
tmp=data[i];
post=0;
while (j<=size && post==0) {
if (j<size) {
if (data[j]<data[j+1])
j+=1;
}
if (tmp>=data[j])
post=1;
else {
data[Math.floor(j/2)]=data[j];
j=2*j;
}
}
data[Math.floor(j/2)]=tmp;
}
data=[0,5,6,4,8,3,2,7,1];
size=9;
process.stdout.write('原始陣列:');
for (i=1; i<size; i++)
process.stdout.write('['+data[i]+'] ');
heap(data,size);
process.stdout.write('排序結果:');
for (i=1; i<size; i++)
process.stdout.write('['+data[i]+'] ');