作者：bake

9-4二元樹節點搜尋

我們先來討論在所建立的二元樹中搜尋單一節點資料。基本上，二元樹在建立的過程中，是依據左子樹<樹根<右子樹的原則建立，因此只須從樹根出發比較鍵值，如果比樹根大就往右，否則由左往下，直到相等就可以找到搜尋的值，如果比到null，無法再前進就代表搜尋不到此值。

二元樹搜尋的演算法

var search=(ptr,val)=> {
     i=1;
     while (true)  {
            if (ptr==null)
                  return null;
             if (ptr.data==val) {
                  process.stdout.write(‘共搜尋 ‘+i+’ 次’+’\n’);
                  return ptr;
              }
              else if (ptr.data>val)
                  ptr=ptr.left;
              else
                  ptr=ptr.right;
              i+=1;
       }
}

JS               binary_search.js

class tree {
	constructor() {
		this.data=0;
		this.left=null;
		this.right=null;
	}
}

var create_tree=(root,val)=> {
	newnode=new tree();
	newnode.data=val;
	newnode.left=null;
	newnode.right=null;
	if (root==null) {
		root=newnode;
		return root;
	}
	else {
		current=root;
		while (current!=null) {
			backup=current;
			if (current.data>val)
				current=current.left;
			else
				current=current.right;
		}
		if (backup.data>val)
			backup.left=newnode;
		else
			backup.right=newnode;
	}
	return root;
}

var search=(ptr,val)=> {
	i=1;
	while (true) {
		if (ptr==null)
			return null;
		if (ptr.data==val) {
			process.stdout.write('共搜尋 '+i+' 次'+'\n');
			return ptr;
		}
		else if (ptr.data>val)
			ptr=ptr.left;
		else
			ptr=ptr.right;
		i+=1;
	}
}

arr=[7,1,4,2,8,13,12,11,15,9,5];
ptr=null;
process.stdout.write('[原始陣列內容]\n');
for (i=0; i<11; i++) {
	ptr=create_tree(ptr,arr[i]);
	process.stdout.write('['+arr[i]+'] ');
}
process.stdout.write('\n');
const prompt=require('prompt-sync')();
const data=parseInt(prompt('請輸入搜尋值：'));
if (search(ptr.data)!=null)
	process.stdout.write('你要找的值 ['+data+'] 有找到！！\n');
else
	process.stdout.write('您要找的值沒找到！！\n');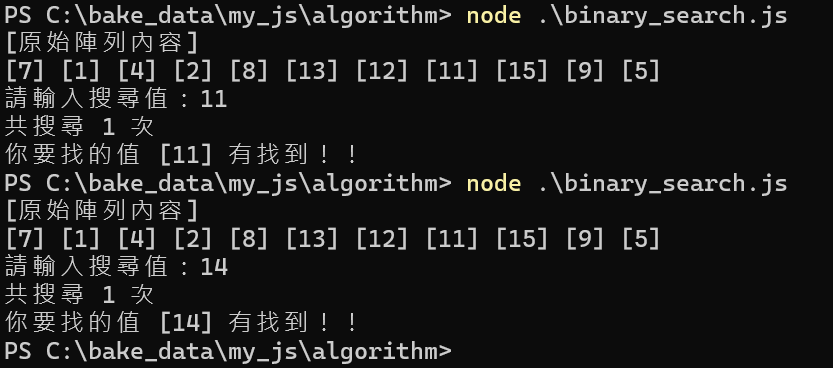

Java Script的程式有問題！

PHP             binary_search.php

class Node {
    public $data;
    public $left;
    public $right;

    public function __construct($data) {
        $this->data = $data;
        $this->left = null;
        $this->right = null;
    }
}
class BinarySearchTree {
    public $root;

    public function __construct() {
        $this->root = null;
    }

    // 插入節點
    public function insert($data) {
        $this->root = $this->insertNode($this->root, $data);
    }

    private function insertNode($node, $data) {
        if ($node === null) {
            return new Node($data);
        }

        if ($data < $node->data) {
            $node->left = $this->insertNode($node->left, $data);
        } elseif ($data > $node->data) {
            $node->right = $this->insertNode($node->right, $data);
        }

        return $node;
    }

    // 中序走訪（in-order traversal）
    public function inorderTraversal($node = null) {
        if ($node === null) {
            $node = $this->root;
        }

        if ($node !== null) {
            $this->inorderTraversal($node->left);
            echo $node->data . " ";
            $this->inorderTraversal($node->right);
        }
    }

    // 搜尋節點
    public function search($data) {
        return $this->searchNode($this->root, $data);
    }

    private function searchNode($node, $data) {
        if ($node === null) return false;

        if ($data == $node->data) return true;

        if ($data < $node->data) {
            return $this->searchNode($node->left, $data);
        } else {
            return $this->searchNode($node->right, $data);
        }
    }
}
$tree = new BinarySearchTree();

$tree->insert(50);
$tree->insert(30);
$tree->insert(70);
$tree->insert(20);
$tree->insert(40);
$tree->insert(60);
$tree->insert(80);

echo "In-order traversal: ";
//$tree->inorderTraversal(); // Output: 20 30 40 50 60 70 80
echo "\n<br>";

echo "Search 60: " . ($tree->search(60) ? "Found" : "Not Found") . "\n<br>"; // Found
echo "Search 90: " . ($tree->search(90) ? "Found" : "Not Found") . "\n<br>"; // Not Found

此程式是用ChatGPT所產生的，但是它的inorderTraversal()函數有問題。