10-4-2 Kruskal 演算法
Kruskal 演算法是將各邊緣線依權值大小由小到大排列,接著從權值最低的邊緣開始架構最小成本擴張樹,如果加入的邊線會造成迴路則捨棄不用,直到加入了n-1個邊線為止。
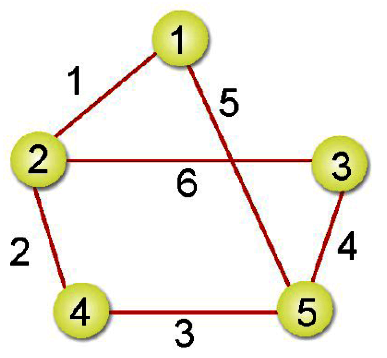
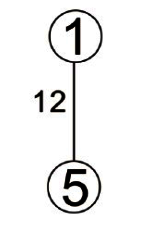
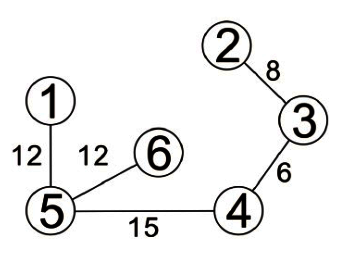
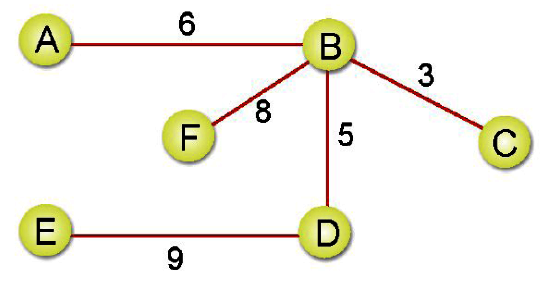
這方法看起來似乎不難,我們直接來看如何以K氏法得到範例下圖中最小成本擴張樹:
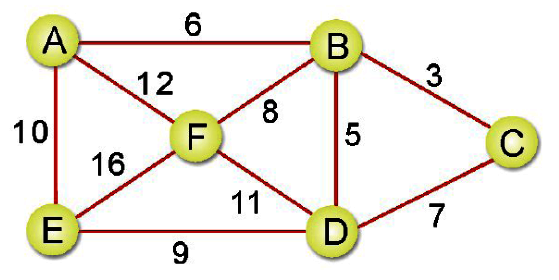
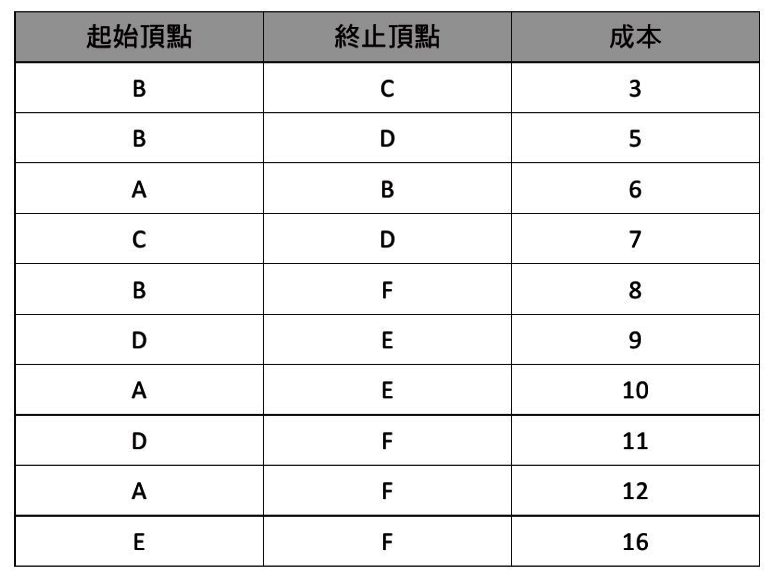
步驟一: 把所有邊線的成本列出並由小到大排序。
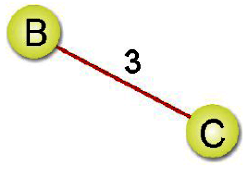
步驟二: 選擇成本最低的一條邊線作為架構最小成本擴張樹的起點。
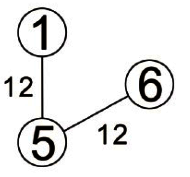
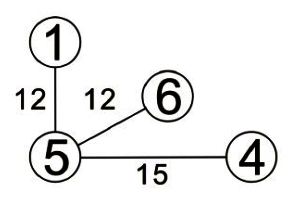
步驟三: 依步驟一所建立的表格,依序加入邊線。
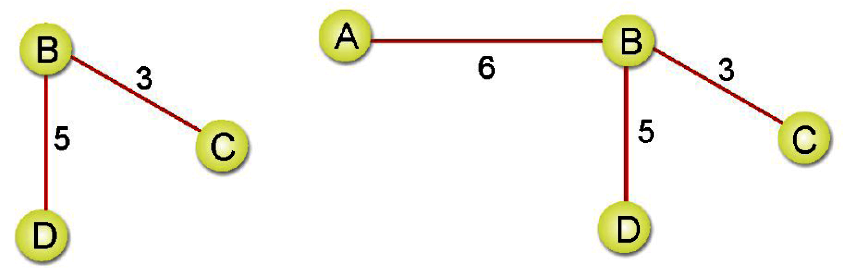
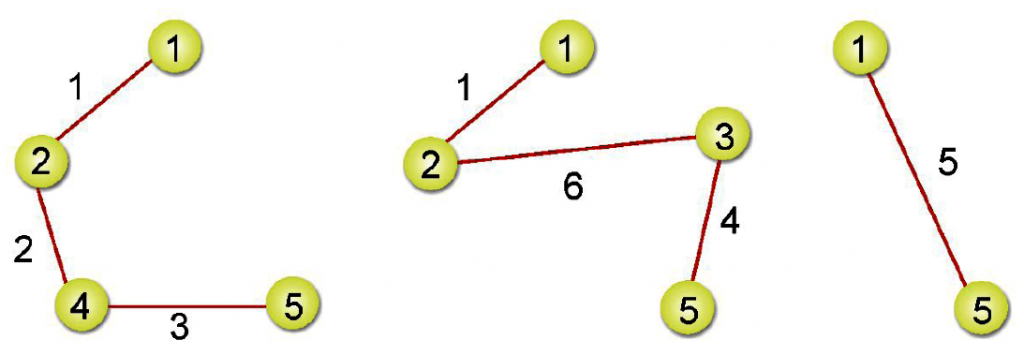
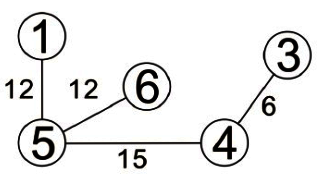
步驟四: C-D加入會形成迴路,所以直接跳過。
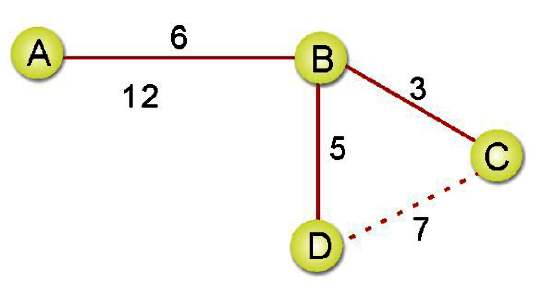
完成圖
Kruskal 法的演算法
const VERTS=6;
class edge {
constructor() {
this.start=0;
this.to=0;
this.find=0;
this.val=0;
this.next=null;
}
}
v=[];
for (let i=0; i<VERTS+1; i++) v[i]=0;
var findmincost=(head)=> {
minval=100;
let ptr=head;
while (ptr!=null) {
if (ptr.val<minval && ptr.find==0) {
minval=ptr.val;
retptr=ptr;
}
ptr=ptr.next;
}
retptr.find=1;
return retptr;
}
var mintree=(head)=> {
let result=0;
let ptr=0;
for (let i=0; i<VERTS; i++)
v[i]=0;
while (ptr!=null) {
mceptr=findmincost(head);
v[mceptr.start]=v[mceptr.start]+1;
v[mceptr.to]=v[mceptr.to]+1;
if (v[mceptr.start]>1 && v[mceptr.to]>1) {
v[mceptr.start]=v[mceptr.start]-1;
v[mceptr.to]=v[mceptr.to]-1;
result=1;
}
else
result=0;
if (result==0) {
process.stdout.write('起點頂點 ['+mceptr.start+'] -> 終止頂點 [' + mceptr.to+'] -> 路徑長度 ['+mceptr.val+']\n');
}
ptr=ptr.next;
}
}
JS kruskal.js
const VERTS=6;
class edge {
constructor() {
this.start=0;
this.to=0;
this.find=0;
this.val=0;
this.next=null;
}
}
v=[];
for (let i=0; i<VERTS+1; i++) v[i]=0;
var findmincost=(head)=> {
minval=100;
let ptr=head;
while (ptr!=null) {
if (ptr.val<minval && ptr.find==0) {
minval=ptr.val;
retptr=ptr;
}
ptr=ptr.next;
}
retptr.find=1;
return retptr;
}
var mintree=(head)=> {
let result=0;
let ptr=head;
for (let i=0; i<VERTS; i++)
v[i]=0;
while (ptr!=null) {
mceptr=findmincost(head);
v[mceptr.start]=v[mceptr.start]+1;
v[mceptr.to]=v[mceptr.to]+1;
if (v[mceptr.start]>1 && v[mceptr.to]>1) {
v[mceptr.start]=v[mceptr.start]-1;
v[mceptr.to]=v[mceptr.to]-1;
result=1;
}
else
result=0;
if (result==0) {
process.stdout.write('起點頂點 ['+mceptr.start+'] -> 終止頂點 [' +
mceptr.to+'] -> 路徑長度 ['+mceptr.val+']\n');
}
ptr=ptr.next;
}
}
data=[[1,2,6],[1,6,12],[1,5,10],[2,3,3],
[2,4,5],[2,6,8],[3,4,7],[4,6,11],
[4,5,9],[5,5,16]];
var head=null;
for (i=0; i<10; i++) {
for (j=1; j<=VERTS+1; j++) {
if (data[i][0]==j) {
newnode=new edge();
newnode.start=data[i][0];
newnode.to=data[i][1];
newnode.val=data[i][2];
newnode.find=0;
newnode.next=null;
if (head==null) {
head=newnode;
head.next=null;
ptr=head;
}
else {
ptr.next=newnode;
ptr=ptr.next;
}
}
}
}
process.stdout.write('--------------------------------------------------\n');
process.stdout.write('建立最小成本擴張樹:\n');
process.stdout.write('--------------------------------------------------\n');
mintree(head);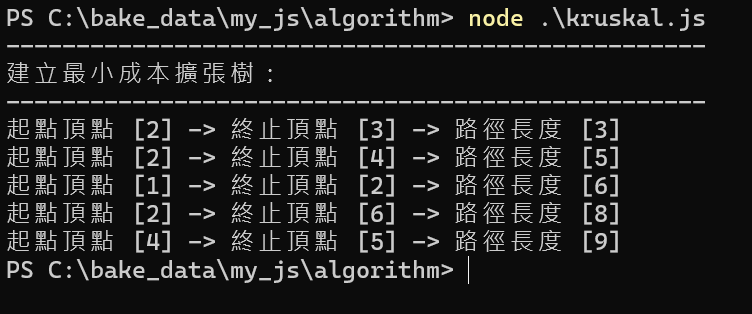
10-5 圖形最短路徑演算法
在一個有向圖形G=(V,E),G中每一個邊都有一個比例常數W(Weight)與之對應,如果想求G圖形中某一個頂點V0到其他頂點的最少W總和之值,這類問題就稱為最短路徑問題(The Shortest Path Problem)。由於交通運輸工具的便利與普及,所以兩地之間有發生運送或者資訊的傳遞下,最短路徑(Shortest Path)的問題隨時都可能因應需求而產生,簡單來說,就是找出兩個端點間可行的捷徑。
我們在上捷中所說明的花費最少擴張樹(MST),是計算聯繫網路中每一個頂點所需的最少花費,但連繫樹中任何倆頂點的路徑不一定是一條花費最少的路徑,這也是本節將研究最短路徑問題的主要理由。以下是在討論最短路徑常見的演算法。
10-5-1 Dijlstra 演算法與A*演算法


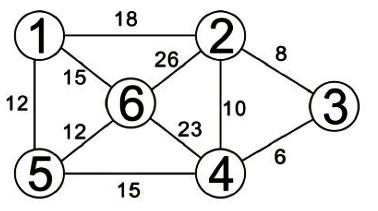
從上述的演算法我們可以推演出如下步驟:

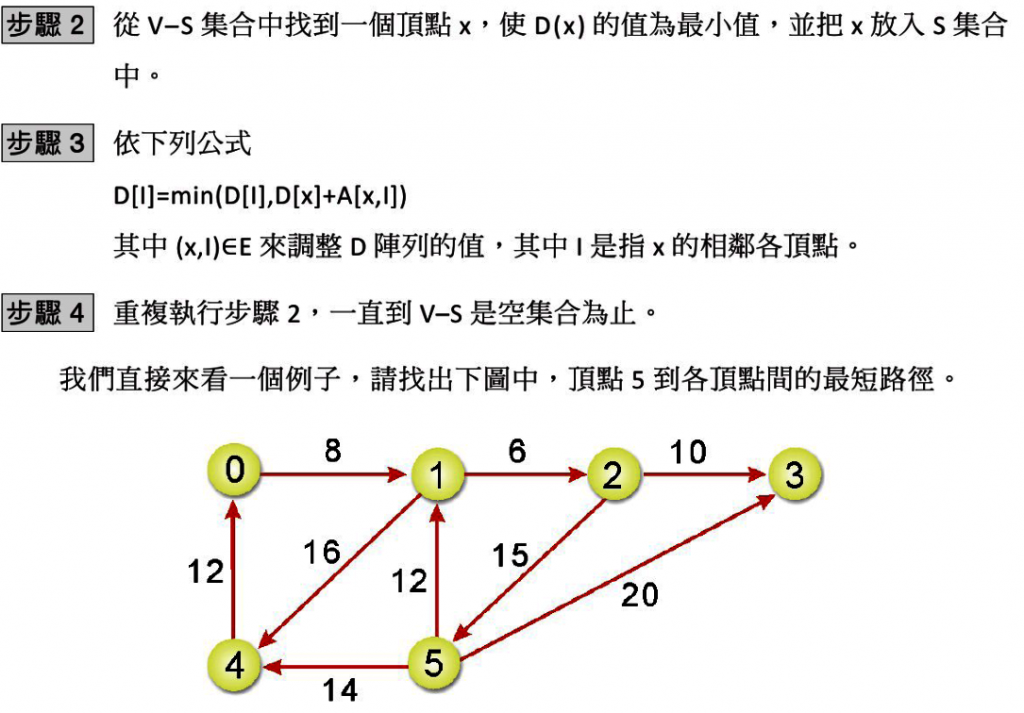


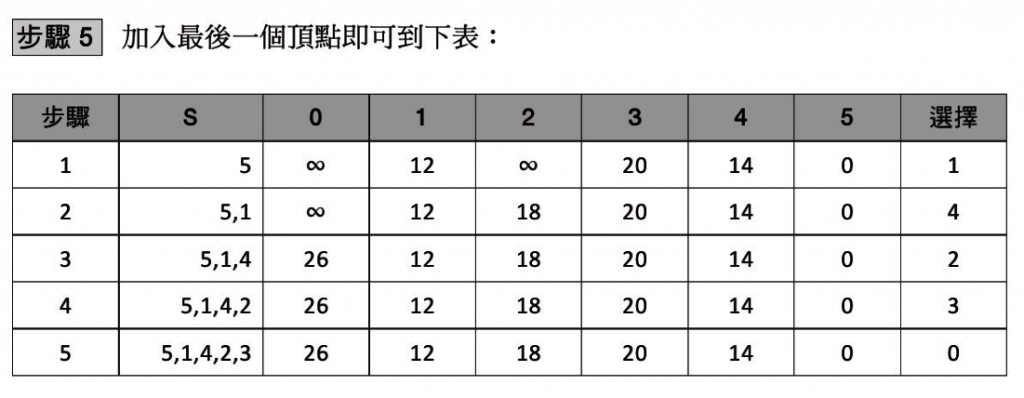
由頂點5到其他各頂點的最短距離為:
頂點5-頂點0:26
頂點5-頂點1:12
頂點5-頂點2:18
頂點5-頂點3:20
頂點5-頂點4:14

JS dijkstra.js
const SIZE=7;
const NUMBER=6;
const INFINITE=99999; //無窮大
var Graph_Matrix=[[0,0,0,0,0,0,0],
[0,0,0,0,0,0,0],
[0,0,0,0,0,0,0],
[0,0,0,0,0,0,0],
[0,0,0,0,0,0,0],
[0,0,0,0,0,0,0],
[0,0,0,0,0,0,0]];
var distance=[];
for (let i=0; i<SIZE; i++) distance[i]=0;
var BuildGraph_Matrix=(Path_Cost)=> {
for (let i=1; i<SIZE; i++) {
for (let j=1; j<SIZE; j++) {
if (i==j)
Graph_Matrix[i][j]=0;
else
Graph_Matrix[i][j]=INFINITE;
}
}
i=0;
while (i<SIZE) {
Start_Point=Path_Cost[i][0];
End_Point=Path_Cost[i][1];
Graph_Matrix[Start_Point][End_Point]=Path_Cost[i][2];
i+=1;
}
}
var shortestPath=(vertexl, vertex_total)=> {
let shortest_vertex=1;
let goal=[];
for (let i=1; i<vertex_total+1; i++) {
goal[i]=0;
distance[i]=Graph_Matrix[vertexl][i];
}
goal[vertexl]=1;
distance[vertexl]=0;
process.stdout.write('\n');
for (let i=1; i<vertex_total; i++) {
shortest_distance=INFINITE;
for (let j=1; j<vertex_total+1; j++) {
if (goal[j]==0 && shortest_distance>distance[j]) {
shortest_distance=distance[j];
shortest_vertex=j;
}
}
goal[shortest_vertex]=1;
for (let j=1; j<vertex_total+1; j++) {
if (goal[j]==0 &&
distance[shortest_vertex]+Graph_Matrix[shortest_vertex]
[j]<distance[j]){
distance[j]=distance[shortest_vertex]+Graph_Matrix[shortest_vertex][j];
}
}
}
}
Path_Cost=[[1,2,29],[2,3,30],[2,4,35],
[3,5,28],[3,6,87],[4,5,42],
[4,6,75],[5,6,97]];
BuildGraph_Matrix(Path_Cost);
shortestPath(1,NUMBER);
process.stdout.write('------------------------------\n');
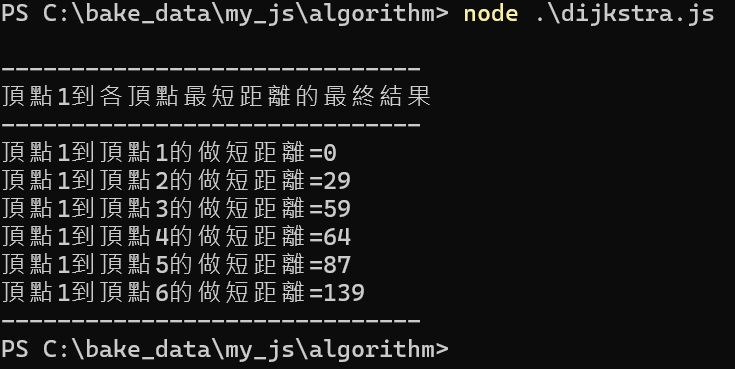
process.stdout.write('頂點1到各頂點最短距離的最終結果\n');
process.stdout.write('------------------------------\n');
for (let j=1; j<SIZE; j++) {
process.stdout.write('頂點1到頂點'+j+'的做短距離='+distance[j]+'\n');
}
process.stdout.write('------------------------------\n');