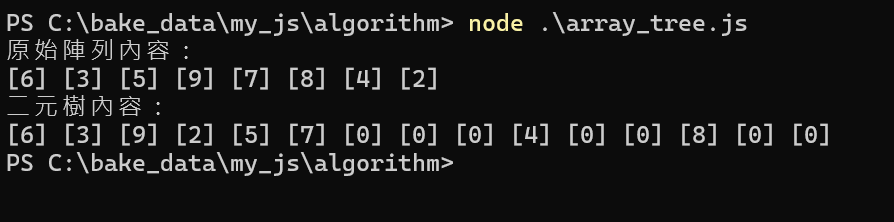
9-3二元樹走訪的入門捷徑
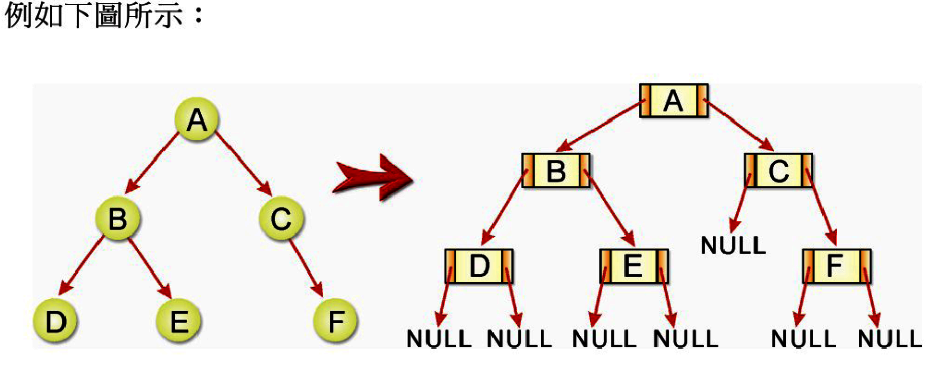
我們知道線性陣列或串列,都只能單向從頭至尾或反向走訪。所謂二元樹的走訪(Binary Tree Traversal),最簡單的說法就是「拜訪樹中所有的節點各一次」,並且在走訪後,將樹中的資料轉化為線性關係。就以下圖一個簡單的二元樹而言,每個節點都可區分為左右兩個分支。
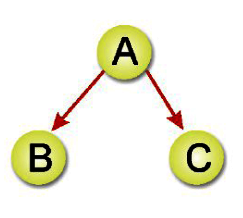
所以共可以有ABC、ACB、BAC、BCA、CAB、CBA等6種走訪方法。如果是依照二元數特性,一律由左向右,那會只剩下三種走訪方式,分別是BAC、ABC、BCA三種。我們通常把這三種方式的命名與規則如下:
1.中序走訪(BAC,Inorder):左子樹->樹根->右子樹
2.前序走訪(ABC,Preorder):樹根->左子樹->右子樹
3.後序走訪(BCA,Postorder):左子樹->右子樹->樹根
對於這三種走訪方式,各位讀者只需要記得樹根位置就不會前中後序給搞混。例如中序法及樹根在中間,前序法是樹根在前面,後序法則是樹跟在後面。而走訪方式也一定是先左子樹後右子樹。以下針對這三種方式,為各位做更詳盡的介紹。
>>中序走訪
中序走訪(Inorder Traversal)也就是從樹的左側逐步向下方移動,直到無法移動,再追蹤此節點,並向右移動一節點。如果無法再向右移動時,可以返回上一層的父節點,重複左、中、右的步驟進行。如下所示:
1.走訪左子樹。
2.拜訪樹根。
3.走訪右子樹。
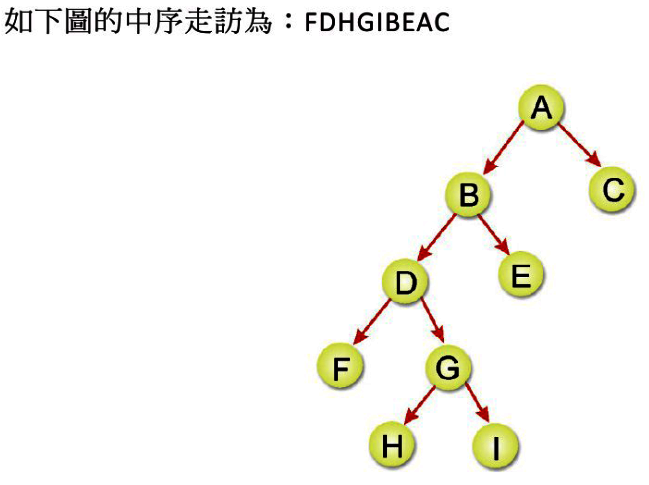
中序走訪的遞迴演算法如下:
var inorder=(ptr)=> {
if(ptr!=null) {
inorder(ptr.left);
process.stdout.write('['+ptr.data+']');
inorder(ptr.right);
}
}
>>後序走訪
後續走訪(Postorder Traversal)走訪的順序是先追蹤左子樹,再追蹤右子樹,最後處理根結點,反覆執行此步驟。如下所示:
1.走訪左子樹。
2.走訪右子樹。
3.拜訪樹根。
如下圖的後序走訪為:FHIGDEBCA
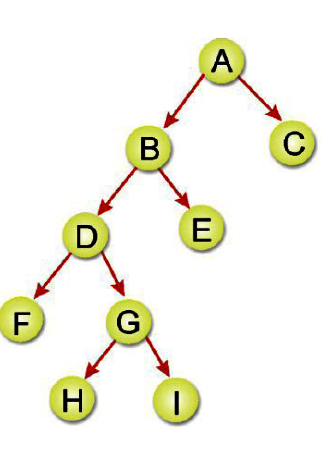
後序走訪的遞迴演算法如下:
var postorder=(ptr)=> { //後序走訪
if (ptr!=null) {
postorder(ptr.left);
postorder(ptr.right);
process.stdout.write(‘[‘+ptr.data+’] ‘);
}
}
>>前序走訪
前序走訪(Preorder Traversal)是從根節點走訪,再往左右移動,無法繼續時,繼續向右方移動,接著再重複執行此步驟。如下所示:
1.拜訪樹根。
2.走訪左子樹。
3.走訪右子樹。
下圖的前序走訪為:ABDFGHIEC

前序走訪的遞迴演算法如下:
var preorder=(ptr)=> {
if (ptr!=null) {
process.stdout.write(‘[‘+ptr.data+’] ‘);
preorder(ptr.left);
preorder(ptr.right);
}
}

JS inorder.js
class tree {
constructor() {
this.data=0;
this.left=null;
this.right=null;
}
}
var inorder=(ptr)=> {
if (ptr!=null) {
inorder(ptr.left);
process.stdout.write('['+ptr.data+'] ');
inorder(ptr.right);
}
}
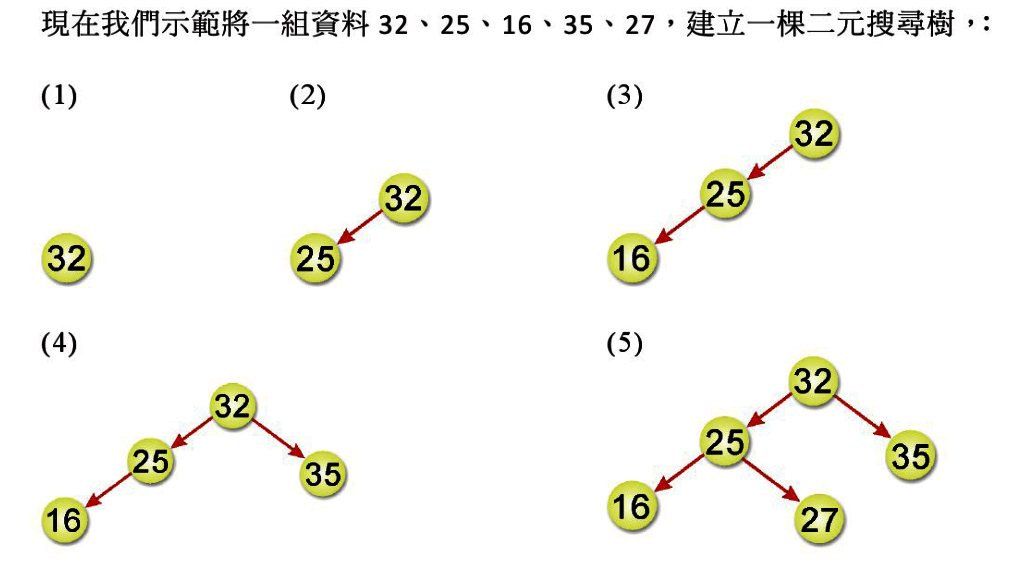
var create_tree=(root,val)=> {
newnode=new tree();
newnode.data=val;
newnode.left=null;
newnode.right=null;
if (root==null) {
root=newnode;
return root;
}
else {
current=root;
while (current!=null) {
backup=current;
if (current.data>val)
current=current.left;
else
current=current.right;
}
if (backup.data>val)
backup.left=newnode;
else
backup.right=newnode;
}
return root;
}
//主程式
data=[5,6,24,8,12,3,17,1,9];
ptr=null;
root=null;
for (i=0; i<9; i++)
ptr=create_tree(ptr,data[i]);
process.stdout.write('================\n');
process.stdout.write('排序完成結果:\n');
inorder(ptr);
process.stdout.write('\n');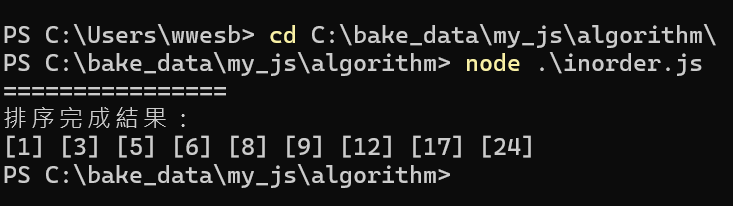
PHP inorder.php
目前,還是沒辦法解決二元樹-20250660
吳老師建議查ChatGPT查查看,inorder-中序尋訪可以解,
但是binary_search的inorder有問題。
class TreeNode {
public $val;
public $left;
public $right;
public function __construct($val) {
$this->val = $val;
$this->left = null;
$this->right = null;
}
}
// 中序走訪函式
function inorderTraversal($node) {
if ($node === null) {
return;
}
// 遞迴走訪左子樹
inorderTraversal($node->left);
// 處理當前節點
echo $node->val . " ";
// 遞迴走訪右子樹
inorderTraversal($node->right);
}
// 建立範例二元樹
// 1
// / \
// 2 3
// / \
// 4 5
$root = new TreeNode(1);
$root->left = new TreeNode(2);
$root->right = new TreeNode(3);
$root->left->left = new TreeNode(4);
$root->left->right = new TreeNode(5);
// 執行中序走訪
echo "中序走訪結果: ";
inorderTraversal($root); // 預期輸出:4 2 5 1 3