圖說演算法-JavaScript – 頁面 8

圖說演算法使用JavaScript(十八)

7-8基數排序法

基數排序法和我們之前所討論到的排序法不一樣，它並不需要進行元素間的比較動作，而是屬於一種分配模式排序方式。基數排序法依照比較的方式。基數排序法依照比較的方向可分為最有效鍵優先(Most Significant Digit First, MSD)和最無效鍵優先(Least Significaant Digit First, LSD)兩種。MSD法是從最左邊的位數開始比較，而LSD則是從最右邊的位數開始比較。

以下的範例我們以LSD將三位數的整數資料來加以排序，它是依個位數、十位數、百位數來進行排序。請直接看以下最無效鍵優先(LSD)例子的說明，便可清楚的知道它的動作原理：

原始資料如下：

JS radix.js

//基數排序法 由小到大排序
var inputarr=(data, size)=> {
	for (i=0; i<size; i++) {
		data[i]=Math.floor(Math.random()*1000);
		//設定data值最大為3位數
	}
}

var showdata=(data, size)=> {
	for (i=0; i<size; i++) process.stdout.write(data[i]+' ');
		console.log();
}

var radix=(data, size)=> {
	for (n=1; n<=100; n=n*10)
	{
		var tmp=new Array();
		for (var i=0; i<10; i++) {
			tmp[i]=new Array();
			for (var j=0; j<10; j++) {
				tmp[i][j]=0;
			}
		}

		for (i=0; i<size; i++) 
		{
			m=Math.floor((data[i]/n))%10;
			tmp[m][i]=data[i];
		}
		k=0;
		for (i=0; i<10; i++)
		{
			for(j=0; j<10; j++)
			{
				if (tmp[i][j] !=0)
				{
					data[k]=tmp[i][j];
					k++;
				}
			}
		}
		process.stdout.write("經過"+n+"位數排序後：");
		showdata(data, size);
	}

}

var data=new Array(100);
for (i=0; i<100; i++) data[i]=0;
const prompt=require('prompt-sync')();
size = prompt('請輸入陣列大小(100以下)：');
process.stdout.write('您輸入的原始資料是：');
console.log();
inputarr(data,size);
showdata(data,size);
radix(data,size);

圖說演算法使用JavaScript(十七)

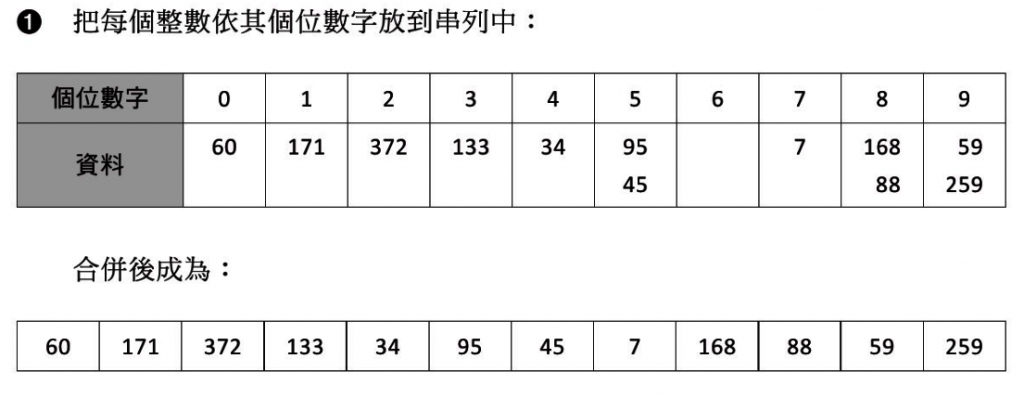
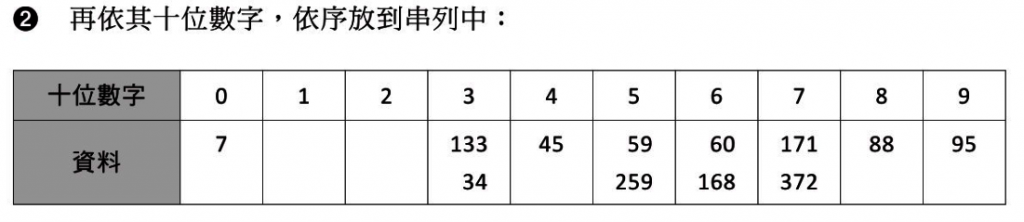
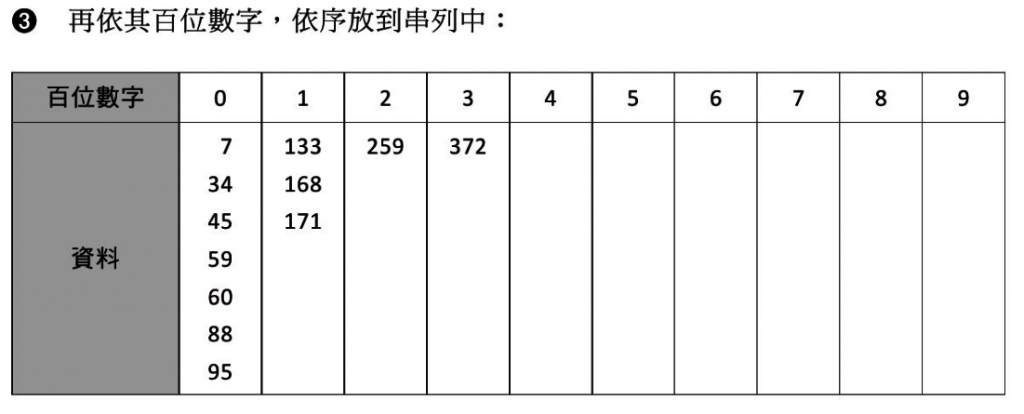
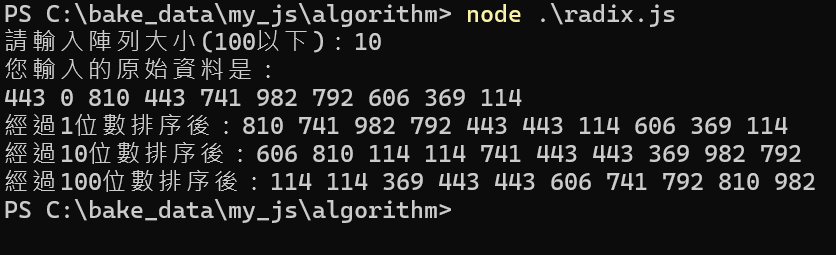
7-6合併排序法

合併排序法(Merge Sort)工作原理乃是針對已排序好的二個或二個以上的數列，經由合併的方式，將其組合成一個大的且已經排序好的數列。步驟如下：

1.將N個長度為1的鍵值成對地合併成N/2個長度為2的鍵值組。
2.將N/2個長度為2的鍵值組成對地合併成N/4個長度為4的鍵值。
3.將鍵值不斷地合併，直到合併成一組長度為N的鍵值組為止。

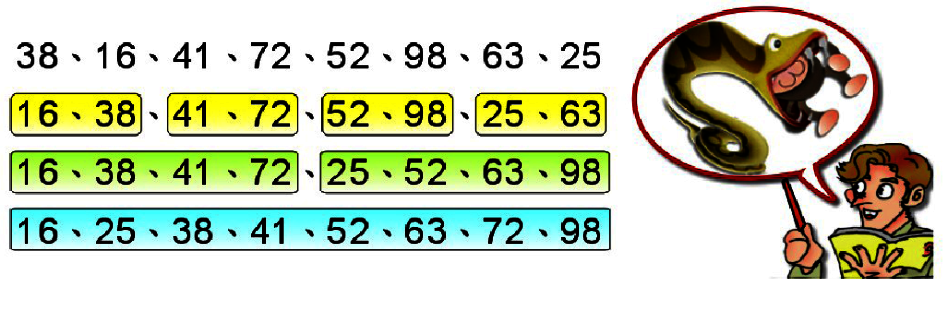
以下利用38、16、41、72、52、98、63、25數列的由小到大排序過程，來說明合併排序法的基本演算流程：

上面展示的合併排序法例子是一種最簡單的合併排序，又稱為2路(2way)合併排序，主要概念是把原來的檔案視作N個已排序妥當且長度為1的數列，再將這些長度為1的兩兩合併，結合成N/2個已排序妥當且長度為2的數列；同樣的作法，再依序兩兩合併，合併成N/4個排序妥當且長度為4的數列….，以此類推，最後合併成一個已排序妥當且長度為N的數列。步驟整理如下：

1.將N個長度為1的數列合併成N/2個已排序妥當且長度為2的數列。
2.將N/2個長度為2的數列合併成N/4個已排序妥當且長度為4的數列。
3.將N/4個長度為4的數列合併成N/8個已排序妥當且長度為8的數列。
4.將N/2i-1個長度為2i-1的數列合併成N/2i個已排序妥當的數列。

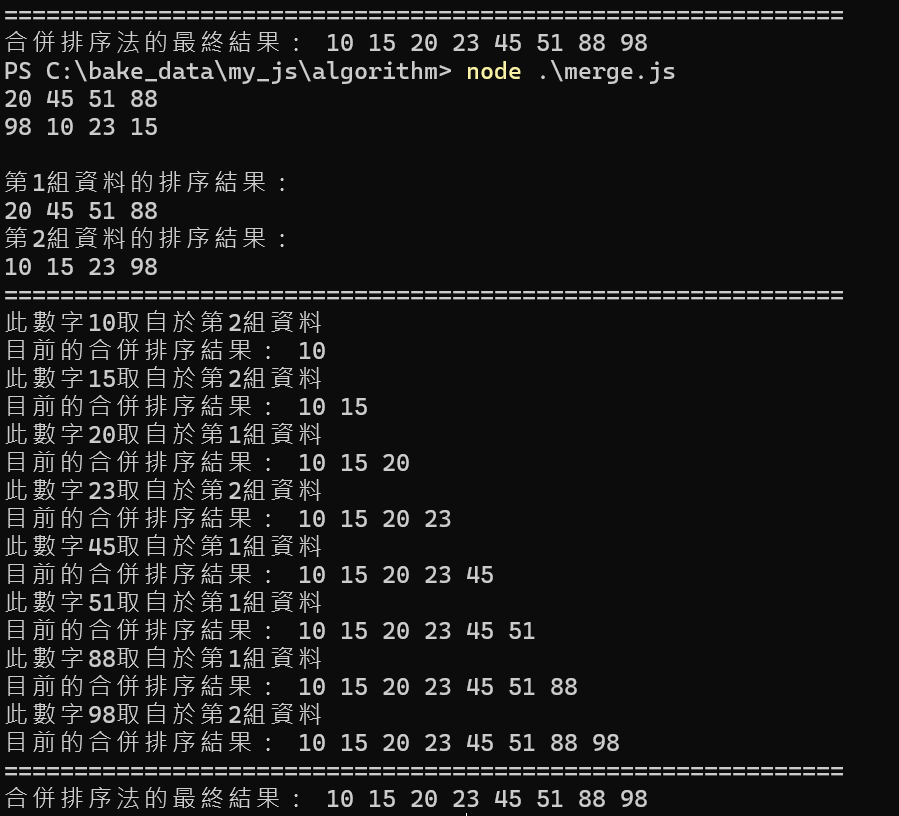
範例：merge.js>請設計一程式，並使用合併排序法來排序。

JS merge.js

//合併排序法(Merge Sort)

//99999為串列1的結束數字不列入排序
list1=[20,45,51,88,99999];
//99999為串列2的結束不列入排序
list2=[98,10,23,15,99999];
list3=[];

for (i=0; i<list1.length-1; i++) process.stdout.write(list1[i]+' ');
console.log();
for (i=0; i<list2.length-1; i++) process.stdout.write(list2[i]+' ');
console.log();

var merge_sort=()=> {

	//先使用選擇排序將兩數列排序，再做合併
	select_sort(list1, list1.length-1);
	select_sort(list2, list2.length-1);
	console.log();
	process.stdout.write('第1組資料的排序結果：');
	console.log();
	for (i=0; i<list1.length-1; i++) process.stdout.write(list1[i]+' ');
	console.log();
	process.stdout.write('第2組資料的排序結果：');
	console.log();
	for (i=0; i<list2.length-1; i++) process.stdout.write(list2[i]+' ');
	console.log();
	
	for (i=0; i<60; i++) process.stdout.write('=');
	console.log();
	
	My_Merge(list1.length-1, list2.length-1);

	for (i=0; i<60; i++) process.stdout.write('=');
	console.log();
	
	process.stdout.write('合併排序法的最終結果： ');

	for (i=0; i<list1.length+list2.length-2; i++)
		process.stdout.write(list3[i]+ ' ');
}

var select_sort=(data, size)=> {
	for (base=0; base<size-1; base++) {
		small=base;
		for (j=base+1; j<size; j++) {
			if (data[j]< data[small]) small=j;
		}
		temp=data[small];
		data[small]=data[base];
		data[base]=temp;
	}
}

var My_Merge=(size1, size2)=> {
	index1 = 0;
	index2 = 0;

	for (index3=0; index3<list1.length+list2.length-2; index3++) {
		if (list1[index1] < list2[index2]) {
			list3.push(list1[index1]);
			index1 +=1;
			process.stdout.write('此數字'+ list3[index3]+ '取自於第1組資料');
		}
		else {
			list3.push(list2[index2]);
			index2 +=1;
			process.stdout.write('此數字'+ list3[index3]+ '取自於第2組資料');
		}
		console.log();
		process.stdout.write('目前的合併排序結果： ');
		for (i=0; i<index3+1; i++) process.stdout.write(list3[i]+ ' ');
		console.log();
	}
}

//主程式開始
merge_sort();

PHP merge.php

$list1=array(88,45,51,20,99999);
$list2=array(98,10,23,15,99999);
$list3=array();

merge_sort($list1, $list2, $list3);

function merge_sort($data1, $data2, $data3) {
	
	echo "第1組原始陣列：";
	print_arr($data1);
	echo "第2組原始陣列：";
	print_arr($data2);
	echo "第3組原始陣列：";
	print_arr($data3);
	echo "<br>";
	
	echo "第1組資料的排序結果：";
	print_arr(select_sort($data1));
	echo "第2組資料的排序結果：";
	print_arr(select_sort($data2));

	for ($i=0; $i<60; $i++){
		echo "=";
	}
	$sort_data1=select_sort($data1);
	$sort_data2=select_sort($data2);

	print_arr(My_Merge($sort_data1, $sort_data2));
}

function select_sort($data) {
	$size=count($data);

	for ($base=0; $base<$size-1; $base++) {
			$small=$base;
			for ($j=$base+1; $j<$size; $j++) {
				if ($data[$j] < $data[$small]) $small=$j;
			}
			$temp=$data[$small];
			$data[$small]=$data[$base];
			$data[$base]=$temp;
		}
		return $data;
}

function  My_Merge($data1, $data2) {
	$index1=0;
	$index2=0;
	$size1=count($data1);
	$size2=count($data2);
	$data3=array();

	for ($index3=0; $index3<$size1+$size2-2; $index3++) {
		if ($data1[$index1] < $data2[$index2]) {
				//array_push($data3, $data1[$index1]);
				$data3[]=$data1[$index1];
				$index1 ++;
				echo "<br>此數字".$data3[$index3]."取自於第1組資料";
		}else{
				//array_push($data3, $data2[$index2]);
				$data3[]=$data2[$index2];
				$index2 ++;
				echo "<br>此數字".$data3[$index3]."取自於第2組資料";
		}

		print_arr($data3);
		
		}
		return $data3;
}

function print_arr($arr) {
	foreach ($arr as $key => $value){
		echo $value." ";
	}
	echo "<br>";
}

7-7快速排序法

快速排序法(Quicksort)是由C.A.R.Hoare所發展的，又稱分割交換排序法，是目前公認最佳的排序法，也是使用分治法(Divide and Conquer)的方式，先是資料中找到一個隨機設定虛擬中間值，並依此中間值的資料將所有打算排序的資料分為兩部分。其中小於中間值的資料放在左邊，而大於中間值的資料放在右邊，再以同樣的方式分別處理左右兩邊的資料，直到排序完為止。操作與分割步驟如下：

假設有n筆R1、R2、R3…Rn紀錄，其鍵值為K1、K2、K3…Kn：
1.先假設K的值為第一個鍵值。
2.由左向右找出鍵值Ki，使得Ki>K。
3.由右向左找出鍵值Kj，使得Kj<K。
4.如果i<j，那麼Ki與Kj交換，並回到步驟2。
5.i>=j則K與Kj交換，並以j為基準點分割成左右部分。然後再針對左右兩邊進行步驟1至5，直到左半邊鍵值=右半邊鍵值為止。

JS quick.js

var inputarr=(data, size)=> {
	for (i=0; i<size; i++) data[i]=Math.floor(Math.random()*100)+1;
}

var showdata=(data, size)=> {
	for (i=0; i<size; i++) process.stdout.write(data[i]+' ');
	console.log();
}

var quick=(d,size,lf,rg)=> {
	//第一筆鍵值為d[lf]
	if (lf<rg) {
		//排序資料的左邊與右邊
		lf_idx=lf+1;
		while (d[lf_idx] < d[lf]) {
			if (lf_idx+1 > size) break;
			lf_idx +=1; 
		}
		rg_idx=rg;
		while (d[rg_idx] > d[lf]) rg_idx -=1;
		while (lf_idx < rg_idx) {
			tmp=d[lf_idx];
			d[lf_idx]=d[rg_idx];
			d[rg_idx]=tmp;
			lf_idx +=1;
			while (d[lf_idx] < d[lf]) lf_idx +=1;
			rg_idx -=1;
			while (d[rg_idx] > d[lf]) rg_idx -=1;
		}
		tmp=d[lf];
		d[lf]=d[rg_idx];
		d[rg_idx]=tmp;

		for (i=0; i<size; i++) process.stdout.write(d[i]+ ' ');
		console.log();
		quick(d,size,lf,rg_idx-1);
		//以rg_idx危機點分成左右兩半以遞迴方式
		quick(d,size,rg_idx+1,rg);
		//分別為左右兩半進行排序直至完成排序
	}
}

var data=new Array(100);
for (i=0; i<100; i++) data[i]=0;
const prompt = require('prompt-sync')();
const size = prompt('請輸入陣列大小(100以下)：');
inputarr (data, size);
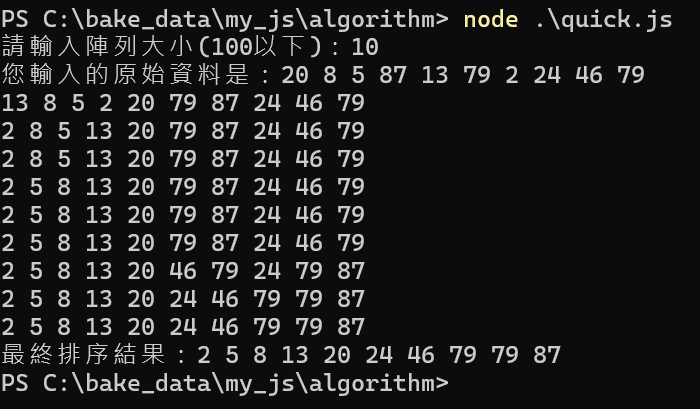
process.stdout.write('您輸入的原始資料是：');
showdata(data, size);
quick(data, size, 0 ,size-1);
process.stdout.write('最終排序結果：');
showdata(data, size);

PHP quick.php

mt_srand((double)microtime()*1000000);
$data =array();

if($_POST['submit'] !='送出') {
echo "
		<center>
     <form method='post' action='{$_SERVER['[PHP_SELF]']}'>
     請輸入陣列大小
     <input name='choice_size' type='text'>
		 <input type='submit' name='submit' value='送出''>
     </form>
    </center>
";
}
else{
	$choice_size=$_POST['choice_size'];
	echo "您輸入的數字：".$choice_size."<br>";
  
	for ($i=0; $i<$choice_size; $i++) {
  		$randval=mt_rand(1,500);
  		//echo $input_num."<br>";
  		//$data[]=$input_num;
  	  if (in_array($randval, $data)) { 
  	  //如果已產生過迴圈重跑
					$i--;
			}else{
			$data[] = $randval; 
			//若無重復則 將亂數塞入陣列
			}
  }
  echo "所選出的數列：<br>";
  print_arr($data);
  echo "--------------------------------------------<br>";

 	quick($data, $choice_size, 0, $choice_size-1);
  echo "--------------------------------------------<br>";
  echo "排列後的數列：<br>";
  //print_arr($sort_data);
  
}

function quick ($d, $size, $lf, $rg) {
	//第一筆鍵值為$d[$lf]
	if ($lf < $rg) {
		//排序資料的左邊與右邊
		$lf_idx=$lf+1;
		while ($d[$lf_idx] < $d[$lf]) {
			if ($lf_idx+1 > $size) break;
			$lf_idx +=1;
		}
		$rg_idx=$rg;
		while ($d[$rg_idx] > $d[$lf]) $rg_idx -=1;
		while ($lf_idx < $rg_idx) {
			$tmp=$d[$lf_idx];
			$d[$lf_idx]=$d[$rg_idx];
			$d[$rg_idx]=$tmp;
			$lf_idx +=1;
			while ($d[$lf_idx] < $d[$lf]) $lf_idx +=1;
			$rg_idx -=1;
			while ($d[$rg_idx] > $d[$lf]) $rg_idx -=1;
		}
		$tmp=$d[$lf];
		$d[$lf]=$d[$rg_idx];
		$d[$rg_idx]=$tmp;
		
		echo "排序中{$k}：";
		print_arr($d);
		quick($d, $size, $lf, $rg_idx-1);
		//以rg_idx為基準點分成左右兩半以遞迴方式
		quick($d, $size, $rg_idx+1, $rg);
		//分別為左右兩半進行排序直至完成排序
	}
	//return $d;
}


function print_arr ($arr) {
	foreach ($arr as $key => $value){
		echo $value." ";
	}
	echo "<br>";
}

後記：目前(20250604)不知道程式哪裡出了問題？排序都有問題。 quick.php

圖說演算法使用JavaScript(十六)

7-4插入排序法

插入排序法insert sort則是將陣列中的元素，逐一與已排序好的資料作比較，如前兩個元素先排好，再將第三個元素插入適當的位置，所以這三個元素仍然是已排序好，接著再將第四個元素加入，重複此步驟，直到排序完成為止。各位可以看做是在一串有序的紀錄R1、R2..Ri，插入新的紀錄R，使得i+1個紀錄排序妥當。

以下利用55、23、87、62、16數列的由小到大排序過程，來說明插入排序法的演算流程。下圖中，在步驟二，以23為基準與其他元素比較後，放到適當位置(55的前面)，步驟三則拿87與其他兩個元素比較後，接著62在比較完前三個數後插入87的前面…，將最後一個元素比較完後即完成排序：

JS insert.js

let SIZE=8;
	//定義陣列大小
var showdata=(data)=> {
	for (k=0; k<8; k++) {
		process.stdout.write(data[k]+' ');
	}
}

var insert=(data)=> {
	for (i=0; i<SIZE; i++) {
		tmp=data[i];
		//tmp用來暫存資料
		no=i-1;
		while (no>=0 && tmp<data[no]) {
			data[no+1]=data[no];
			//就把所有元素往後推一個位置
			no-=1;
		}
		data[no+1]=tmp;
		//最小的元素放到第一個元素
	}
}
data=[16,25,39,27,12,8,45,63];
console.log('原始陣列是：');
showdata(data);
insert(data);
console.log();
console.log('排序後陣列是：');
showdata(data);

PHP insert.php

$data=array(16,25,39,27,12,8,45,63);
$count=count($data);

echo "原始陣列：<br>";
showdata($data);

$new_data=insert($data);

echo "<br>排列後的陣列：<br>";
showdata($new_data);

function insert($arr) {
	$count=count($arr);
	//計算陣列大小
	for ($i=0; $i<$count; $i++) {
		$tmp=$arr[$i];
		//用tmp來暫存資料
		$no=$i-1;
		while ($no>=0 && $tmp<$data[$no]){
			$data[$no+1]=$data[$no];
			//就把所有元素往後推一個位置
			$no--;
		}
		$data[$no+1]=$tmp;
		//最小的元素放到第一個元素  
	}
	return $data;
}


function showdata($arr){
	foreach($arr as $key=>$value){
		echo $value."、";
	}
	echo "<br>";
}

7-5謝耳排序法

我們知道如果原始紀錄的鍵值大部分以排序好的情形下，插入排序法或非常有效率，因為它無須做太多的資料搬移動作。[謝耳排序法]是D.L.Shell在1959年7月所發明的一種排序法，可以減少插入排序法中資料搬移的次數，以加速排序進行。排序的原理是將資料分成特定間隔的幾個小區塊，以插入排序法排完區塊內的資料後再漸漸減少間隔的距離。

以下利用63、92、27、36、45、71、58、7數列的由小到大排序過程，來說明謝耳排序法的演算過程。

範例：shell.js>請設計一程式，並使用謝耳排序法來將以下的數列排序：
16,25,39,27,12,8,45,63

JS shell.js

let SIZE=8;

var showdata=(data)=> {
	for (i=0; i<SIZE; i++) {
		process.stdout.write(data[i]+ ' ');
	}
	console.log();
}

var shell=(data, size)=> {
	k=1;
	//k列印計數
	jmp=parseInt(size/2);
	while (jmp !=0) {
		for (i=jmp; i<size-1; i++) {
			//i為掃描次數 jmp為設定間距位移量
			tmp=data[i];
			//tmp用來暫存資料
			j=i-jmp;
			//以j來定位比較的元素
			while (tmp<data[j] && j>=0) {
				//插入排序法
				data[j+jmp] = data[j];
				j=j-jmp;
			}
			data[jmp+j]=tmp;
		}
		process.stdout.write('第 '+k+' 次排序過程：');
		k=k+1;
		showdata(data);
		console.log('------------------------------------');
		jmp=parseInt(jmp/2);
		//控制迴圈數
	}
}

data=[16,25,39,27,12,8,45,63];
process.stdout.write('原始陣列是：     ');
showdata(data);
console.log('-------------------------------------');
shell(data, SIZE);

PHP shell.php

$data=array(16,25,39,27,12,8,45,63);
echo "原始陣列：<br>";
print_arr($data);
echo "----------------------------<br><br>";


$size=count($data);
$new_data=shell_sort($data, $size);

echo "<br>排序後的陣列：<br>";
print_arr($new_data);

function shell_sort($arr, $size) {
	$k=1;
	//k列印計數
	$jmp=intval($size/2);
	
	while($jmp!=0) {
		for($i=$jmp; $i<$size-1; $i++) {
			//i為掃描次數 jmp為設定間距位移量
			$tmp=$arr[$i];
			//tmp用來暫存資料
			$j=$i-$jmp;
			//以j來定位比較的元素
			while ($tmp<$arr[$j] && $j>=0) {
				//插入比較法
				$arr[$j+$jmp]=$arr[$j];
				$j=$j-$jmp;
				isset($arr[$j])?$arr[$j]=$arr[$j]:$arr[$j]=null;
				//偵測$arr[$j]的key值是否為正確
				//echo $j."<br>";
			}
			$arr[$jmp+$j]=$tmp;
		}
		echo "第".$k."次排序過程<br>";
		$k++;
		print_arr($arr);
		$jmp=intval($jmp/2);
		//控制迴圈數
	}
	
	return $arr;	
}

function print_arr($arr) {
	foreach ($arr as $key => $value){
		echo $value." ";
	}
	echo "<br>";
}

一	二	三	四	五	六	日
« 八月
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30