10-3 圖形走訪的訣竅
樹的追蹤目的是欲拜訪樹的每一個節點一次,可用的方法有中序法、前序法和後序法等三種。而圖形追蹤的定義如下:
一個圖形G=(V,E),存在某一頂點vEV,我們希望從v開始,經由此節點相鄰的節點兒去拜訪G中其他節點,這稱之為(圖形追蹤)。也就是從某一個頂點V1開始,走訪可以經由V1到達的頂點,接著在走訪下一個頂點直到全部的頂點走訪完畢為止。
在走訪的過程中可能會重複經過某些頂點及邊線。經由圖形的走訪可以判斷該圖形是否連通,並找出連通單元及路徑。圖形走訪的方法有兩種:(先深後廣走訪)及(先廣後深走訪)。
10-3-1 先深後廣走訪法
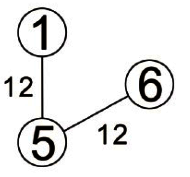
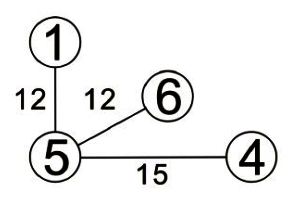
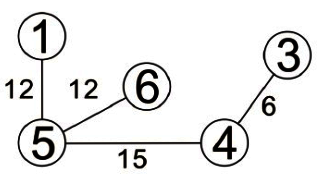
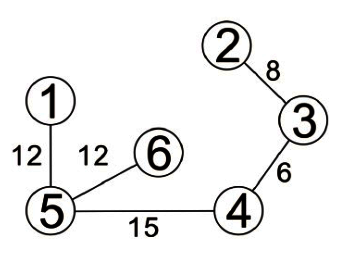
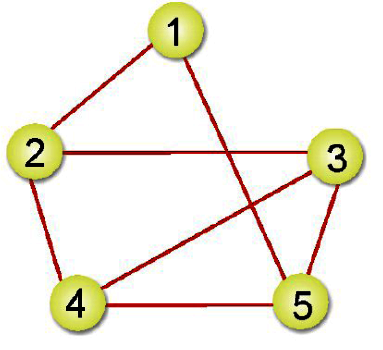
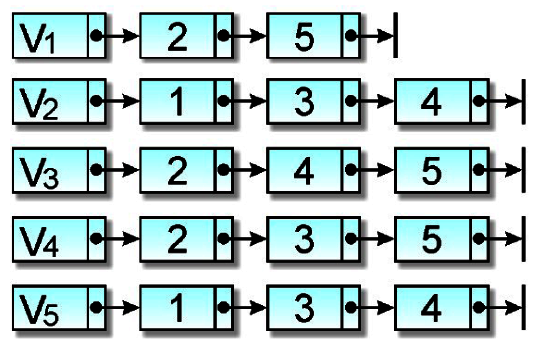
先身後廣走訪的方式有點類似前序走訪。適從圖形的某一頂點開始走訪,被拜訪過的頂點就作上已拜訪記號,接著走訪此頂點的所有相鄰且未拜訪過的頂點中的任一個頂點,並作上已拜訪的記號,再以該點為新的起點繼續進行先深厚廣的搜尋。
這種圖形追蹤方法結合了遞迴及堆疊兩種資料結構的技巧,由於此方法會造成無窮迴路,所以必須加入一個變數,判斷該點是否已經走訪完畢。我們以下徒來看看這個方法的走訪過程。
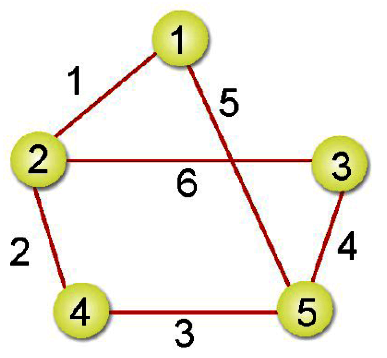
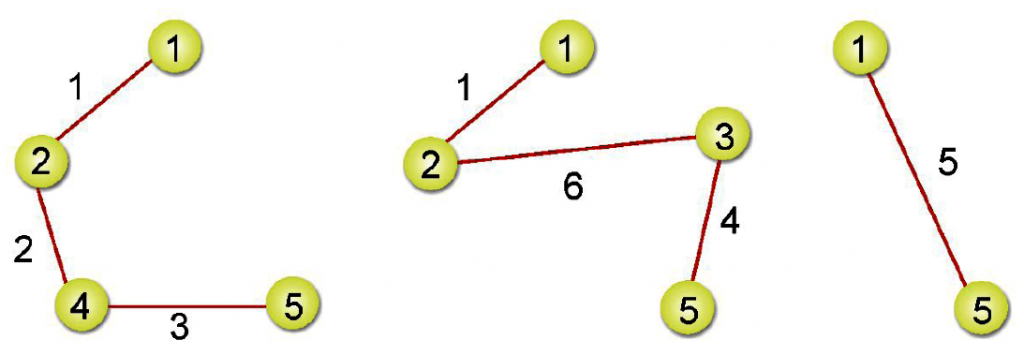
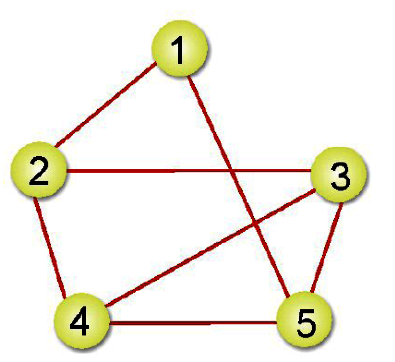
故先深後廣的走訪順序為:頂點1、頂點2、頂點3、頂點4、頂點5。
深度優先函數的演算法如下:
var DFs=(current)=> {
run[current] = 1;
process.stdout.write(“[“+current+”]”);
while (Head[current].first) != null) {
if (run[Head[current].first.x] == 0)
Dfs(Head[current].first.x);
Head[current].first = Head[current].first.next;
}
}
JS dfs.js
class Node {
constructor(x) {
this.x = x;
this.next = null;
}
}
class GraphLink {
constructor() {
this.first = null;
this.last = null;
}
IsEmpty() {
return this.first == null;
}
Print() {
let current = this.first;
while (current != null) {
process.stdout.write('['+current.x+'] ');
current = current.next;
}
process.stdout.write('\n');
}
Insert(x) {
let newNode = new Node(x);
if (this.IsEmpty()) {
this.first = newNode;
this.last = newNode;
}
else {
this.last.next = newNode;
this.last = newNode;
}
}
}
run=[];
Head=[];
for (i=0; i<9; i++)
Head[i] = new GraphLink();
var DFs=(current)=> {
run[current] = 1;
process.stdout.write("["+current+"]");
while ((Head[current].first) != null) {
if (run[Head[current].first.x] == 0)
DFs(Head[current].first.x);
Head[current].first = Head[current].first.next;
}
}
Data=[];
Data=[[1,2],[2,1],[1,3],[3,1],[2,4],
[4,2],[2,5],[5,2],[3,6],[6,3],
[3,7],[7,3],[4,5],[5,4],[6,7],
[7,6],[5,8],[8,5],[6,8],[8,6]];
run=[];
Head=[];
for (i=0; i<9; i++)
Head[i]=new GraphLink();
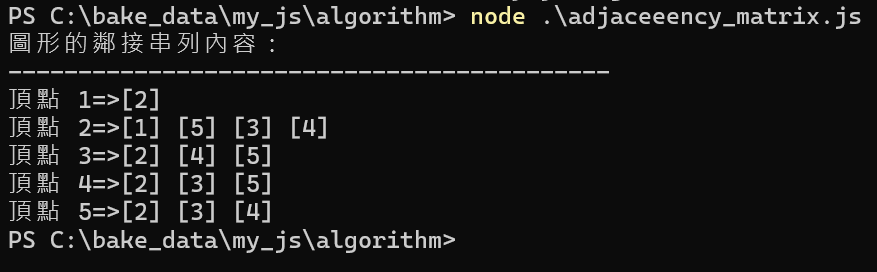
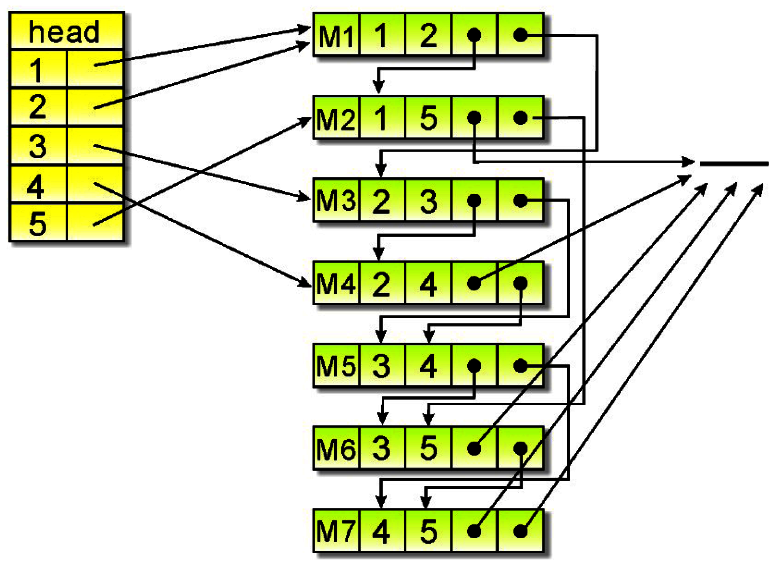
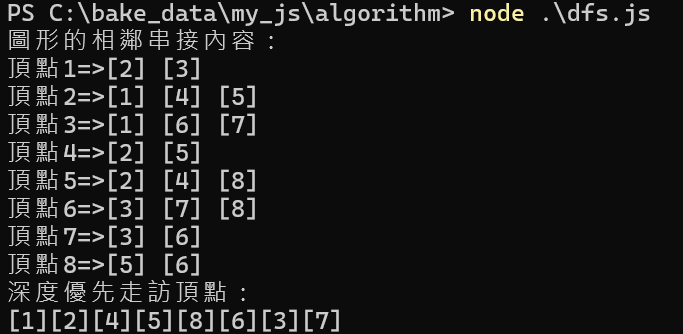
process.stdout.write("圖形的相鄰串接內容:\n");
for (let i=1; i<9; i++) {
run[i]=0;
process.stdout.write('頂點'+ i +'=>');
Head[i] = new GraphLink();
for (j=0; j<20; j++) {
if (Data[j][0]==i) {
DataNum = Data[j][1];
Head[i].Insert(DataNum);
}
}
Head[i].Print();
}
process.stdout.write("深度優先走訪頂點:\n");
DFs(1);
process.stdout.write('\n');
10-3-2 先廣後深搜尋法
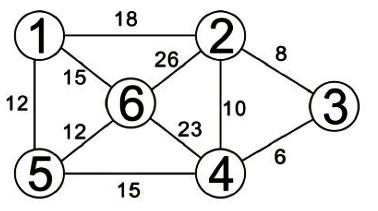
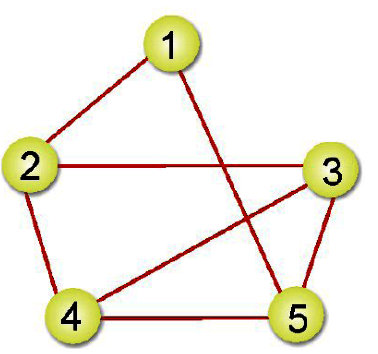
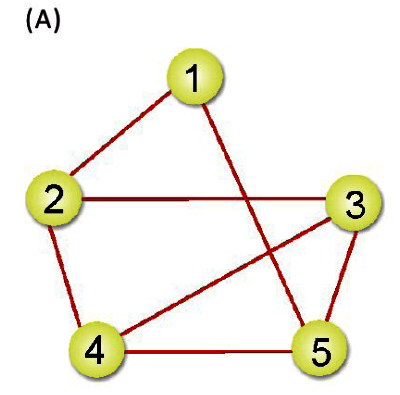
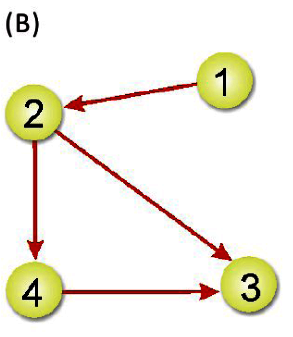
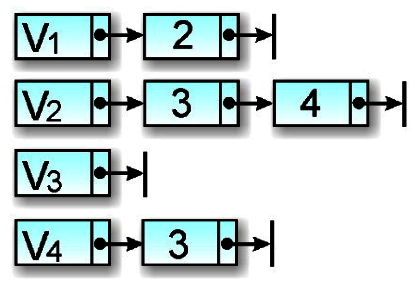
之前所談到先深候廣是利用堆疊及遞迴的技巧來走訪圖形,而先廣後深(Breadth-First Search, BFS)走訪方式則是以佇列及遞迴來走訪,也是從圖形的某一頂點開始走訪,被拜訪過的頂點就做以拜訪的記號。接著走訪此頂點的所有相鄰且為拜訪過的頂點中任意一個頂點,並做上已拜訪的記號,再以該點為新的起點繼續進行先廣後深的搜尋。我們以下圖來看看BFS的走訪過程:
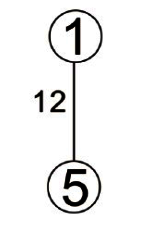
所以,先廣後深的走訪順序為:頂點1、頂點2、頂點5、頂點3、頂點4。
先廣後深函數的演算法如下:
var bfs=(current)=> {
enqueue(current);
run[current]=1;
process.stdout.write(‘[‘+current+’]’);
while (front!=rear) {
current=dequeue();
tempnode=Head[current].first;
while (tempnode!=null) {
if (run[tempnode.x]==0) {
enqueue(tempnode.x);
run[tempnode.x]=1;
process.stdout.write(‘[‘+tempnode.x+’]’);
}
tempnode=tempnode.next;
}
}
}
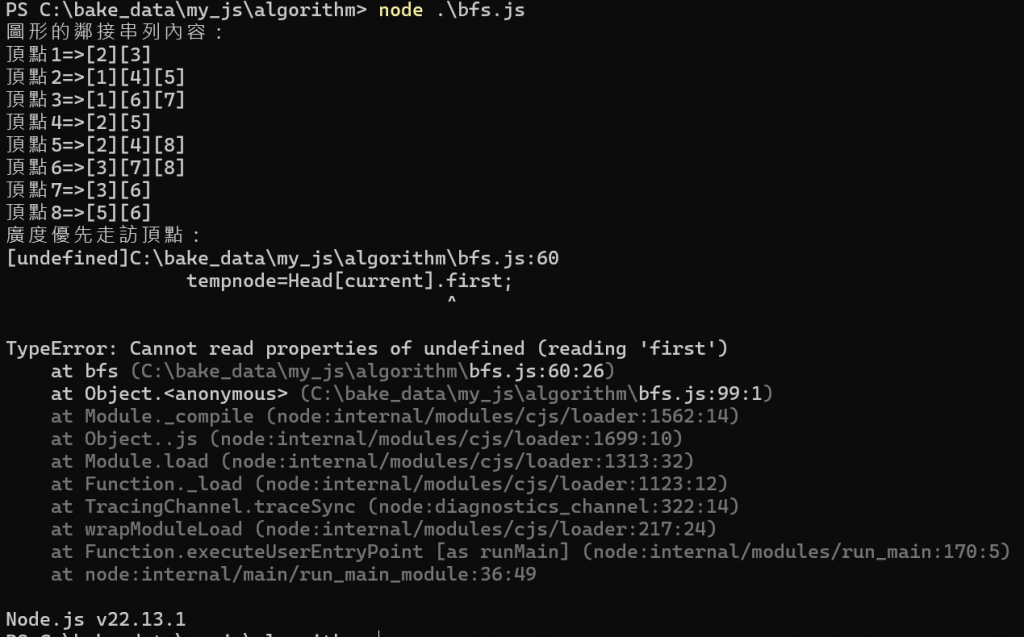
書本範例程式有問題 bfs.js